Surface Area Integration problems
Surface Area of a Solid Integration problem example
Find the Surface Area of a solid generated by revolving the curve
, from 
to 
, about the x-axis.
Solution to this calculus Surface Area of a Solid Integration practice problem is provided in the video below!
Arc Length of a Curve Integration problems
Arc Length of a Curve Integration problem example
Find the Arc Length of a curve 
, from to 
Solution to this calculus Arc Length of a Curve Integration practice problem is provided in the video below!
Area Between Curves Integration problems
Area Between Curves Integration problem example
Find the area bounded by two curves 
and 
Solution to this calculus Area Between Curves Integration practice problem is provided in the video below!
Projectile Motion calculus problems
Projectile Motion In Two Dimensions problem example
An object is launched at angle 
from the horizontal with initial speed Vo = 98 meters per second. Determine the time of flight and the horizontal range of the projectile.
Solution to this Calculus Projectile Motion practice problem is provided in the video below!
Projectile Motion “Baseball Pitcher” example question
A baseball pitcher releases the ball horizontally from a height of 6 feet with an initial velocity of 130 feet per second. Find the height of the ball when it reaches home plate 60 feet away.
Solution to this Calculus Projectile Motion practice problem is provided in the video below!
Theoretical Projectile Motion example
Show that an object dropped from a height of H feet will hit the ground at time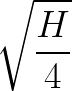 
seconds with impact velocity 
feet per second.
Solution to this Calculus Projectile Motion practice problem is provided in the video below!
Disks Washers Cylindrical Shells Volume of the Solid Integration problems
Volume of the Solid by Revolution DISK Integration Method example
Revolve the region under a curve
on the interval [0, 4] about the x-axis and find the volume of the resulting solid.
Solution to this Volume of the Solid by Rotation practice problem is provided in the video below!
Volume of the Solid by Rotation DISK Integration Method example problem
Find the volume of the solid resulting from revolving the region bounded by the lines
and 
from to 
about the y-axis.
Solution to this Volume of the Solid by Revolution practice problem is provided in the video below!
Volume of the Solid by Revolution WASHER Integration Method example question
Find the volume of the solid resulting from revolving the region bounded by lines
, and ,
about the line 
Solution to this Volume of the Solid by Rotation practice problem is provided in the video below!
Volume of the Solid by Rotation WASHER Integration Method example #2
Find the volume of the solid resulting from revolving the region bounded by lines
, and ,
about the x-axis.
Solution to this Volume of the Solid by Revolution practice problem is provided in the video below!
Volume of the Solid by Rotation CYLINDRICAL SHELL Integration Method example problem
Revolve the region bounded by the graphs of 
and 
in the first quadrant about the y-axis using Cylindrical Shells and find the volume of the resulting solid.
Solution to this Volume of the Solid by Revolution practice problem is provided in the video below!
Volume of the Solid by Revolution WASHER & SHELL Integration Method example question
Find the volume, using Washer and Cylindrical Shell methods, of the solid formed by revolving the region bounded by curves
and 
about the line 
Solution to this Volume of the Solid by Rotation practice problem is provided in the video below!
The Principle of Mathematical Induction problems
The Principle of Mathematical Induction Equality problem example
Prove the following statement by Mathematical Induction:
2 + 4 + 6 + … + 2n = n(n + 1)
Solution to this Mathematical Induction Proof practice problem is provided in the video below!
The Principle of Mathematical Induction Equality Proof example question
Prove the following sequence statement by Mathematical Induction:
3 + 7 + 11 + … + (4n – 1) = n(2n + 1)
Solution to this Mathematical Induction Proof practice problem is provided in the video below!
Exponents & Principle of Mathematical Induction Equality example
Prove the given statement by using Mathematical Induction:
1 + 3 + 32 + … + 3n – 1 =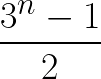 
Solution to this Mathematical Induction Proof practice problem is provided in the video below!
Exponents & Principle of Mathematical Induction Equality example problem #2
Prove the statement below by Mathematical Induction:
13 + 23 + 33 + … + n3 = 
Solution to this Mathematical Induction Proof practice problem is provided in the video below!
Fractions & Principle of Mathematical Induction Equality example question
Show the given sequence statement holds true by using Mathematical Induction:
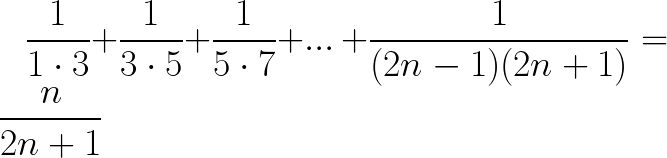
Solution to this Mathematical Induction Proof practice problem is provided in the video below!
Nth Term of Geometric Sequence Formula Proof with Principle of Mathematical Induction
Prove the following formula that finds the Nth term of a Geometric Sequence by using the Principle of
Mathematical Induction:
Solution to this Principle of Mathematical Induction Proof practice problem is provided in the video below!
EXTENDED Principle of Mathematical Induction Inequality example
Prove the following Square Root sequence inequality statement by using the Extended Principle of
Mathematical Induction:
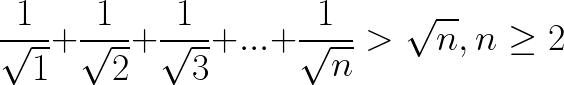
Solution to this Extended Principle of Mathematical Induction Proof practice problem is provided in the video below!
Rotation of Axes problems
Angle of Rotation of Axes problem example
Find an appropriate angle through which to rotate axes to eliminate the xy term in the equation
Solution to this Rotation of Axes practice problem is provided in the video below!
COORDINATE Equations of Rotation of Axes example question
Find the Transformation Equations to rotate axes through an appropriate angle to eliminate the xy term in the equation
Solution to this Rotation of Axes practice problem is provided in the video below!
New Axes of Rotation EQUATION example
Find the Equation into which
is transformed when there is rotation of the axes through an appropriate angle to eliminate the xy term in the given equation.
Solution to this Rotation of Axes practice problem is provided in the video below!
Hyperbola Equation problems
Equation of a Hyperbola problem example
Analyze and sketch Graph of the Hyperbola:
x2 – y2 + 6x + 34 = 0
Solution to this Equation of Hyperbola practice problem is provided in the video below!
Equation of Hyperbola ECCENTRICITY example question #2
Find the Eccentricity of the Hyperbola:
Solution to this Eccentricity of a Hyperbola practice problem is provided in the video below!
Equation of a Hyperbola example #3
Find the equation of a Hyperbola
(a) with vertices (0, ±12) and asymptotes y = ±3x
(b) with foci (3, 6) and (11, 6) and eccentricity 
Solution to this Equation of Hyperbola practice problem is provided in the video below!
Ellipse Equation problems
Equation of an Ellipse problem example
Analyze and Sketch the graph of the Ellipse given by
25x2 + 16y2 + 100x – 96y = 156
Solution to this Equation of Ellipse practice problem is provided in the video below!
Eccentricity of Ellipse example question #2
Find the Eccentricity for
Solution to this Equation of an Ellipse practice problem is provided in the video below!
Equation of an Ellipse with Vertices and Eccentricity example #3
Find the equation of an Ellipse with
(a) major vertices (±4, 0) and eccentricity 
(b) minor vertices (-3, 4) and (1, 4) and eccentricity 
Solution to this Equation of Ellipse practice problem is provided in the video below!
Equation of Ellipse example problem #4
Use the definition of an ellipse PF1 + PF2 = 2a directly to find the equation of an ellipse with foci (0, 0) and (4, 0 ) and major axis 2a = 6.
Solution to this Equation of an Ellipse practice problem is provided in the video below!
Recent Comments