Home » Linear Algebra
Category Archives: Linear Algebra
Eigenvalues & Eigenvectors problems in Linear Algebra
Eigenvalue of Matrix example question
Find the corresponding Eigenvalue of the following matrix A given the Eigenvector x.
A = 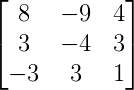
x = ![]()
Solution to this Linear Algebra practice problem is given in the video below!
Basis for Eigenspace of Matrix example problem
Find the Characteristic Equation and Bases for the Eigenspaces of the given matrix A.
A = 
Solution to this Linear Algebra practice problem is given in the video below!
General Vector Spaces problems in Linear Algebra
Real Vector Space example question
Determine whether the given set equipped with the given operations is a vector space.
The set of all triplets of real numbers with the standard vector addition but with scalar multiplication defined by
k(x, y, z) = (k2x, k2y, k2z)
Solution to this Linear Algebra practice problem is given in the video below!
Subspace example problem
Determine whether the following are subspaces of R3:
(a) All vectors of the form (a, 0, 0)
(b) All vectors of the form (a, 1, 0)
(c) All vectors of the form (a, b, c) where b = a + c
(d) All vectors of the form (a, b, c) where c = a ![]() b
b
(e) All vectors of the form (a, ![]() a, 0)
a, 0)
Solution to these Linear Algebra practice problems is given in the video below!
Linear Combination example
Which of the following are linear combinations of u = (1, ![]() 3, 2) and v = (1, 0,
3, 2) and v = (1, 0, ![]() 4)?
4)?
(a) (0, ![]() 3, 6)
3, 6)
(b) (3, ![]() 9,
9, ![]() 2)
2)
(c) (0, 0, 0)
(d) (1, 6, ![]() 16)
16)
Solution to these Linear Algebra practice problems is given in the video below!
Vector Span example question
Determine whether the given vector spans R3:
v1 = (1, 2, 3)
v2 = (2, 0, 0)
v3 = (![]() 2, 1, 0)
2, 1, 0)
Solution to this Linear Algebra practice problem is given in the video below!
Linear Independence example problem
Determine whether the following vectors in R4 are linearly dependent:
(1, 2, ![]() 2, 1)
2, 1)
(3, 6, ![]() 6, 3)
6, 3)
(4, ![]() 2, 4, 1)
2, 4, 1)
Solution to this Linear Algebra practice problem is given in the video below!
Basis of Vector Set example
Determine whether the following set of vectors form a basis in R3:
(1, 0, 0)
(2, 2, 0)
(3, 3, 3)
Solution to this Linear Algebra practice problem is given in the video below!
Basis & Dimension of Solution Space example question
Find a basis for the solution space of the homogeneous linear system, and find the dimension of that space.
2x1 + x2 + 3x3 = 0
x1 + 5x3 = 0
x2 + x3 = 0
Solution to this Linear Algebra practice problem is given in the video below!
Change of Basis example problem
Consider the bases
B = {u1, u2} and B’ = {u1‘, u2‘} for R2,
where
u1 = ![]()
u2 = ![]()
u1‘ = ![]()
u2‘ = ![]()
Find the transition matrix from B to B’.
Solution to this Linear Algebra practice problem is given in the video below!
Subspace Basis example
Find a basis for the subspace of R4 spanned by the given vectors
(2, 4, ![]() 2, 3)
2, 3)
(![]() 2,
2, ![]() 2, 2,
2, 2, ![]() 4)
4)
(1, 3, ![]() 1, 1)
1, 1)
Solution to this Linear Algebra practice problem is given in the video below!
Rank of Matrix example question
Are there values of r and s for which the given matrix has rank 1 or rank 2?
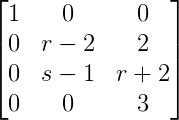
Solution to this Linear Algebra practice problem is given in the video below!
Matrix Inverse problems in Linear Algebra
2×2 Matrix Inverse using Determinant example
A = 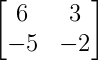
D = 
B = 
Find Inverses of all these 3 matrices, A-1, D-1, B-1, by using their respective determinants.
Solution to this Linear Algebra practice problem is given in the video below!
Matrix Inverse using Identity Matrix example problem
Find the Inverse, if it exists, of the following square matrices by using their Identity Matrix.
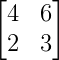

Solution to these Linear Algebra Identity Matrix Inverse practice problems is given in the video below!
System Solution using Matrix Inverse example question
Find the solution to the following system of linear equations by using the product of the Inverse of a coefficient matrix and augmented matrix column.
3x1 + 5x2 = 2
x1 + 2x2 = 3
Solution to this Linear Algebra Matrix Inverse practice problem is given in the video below!
Find Linear Equation using Matrix Inverse example
Use Matrix Inverse to find an Equation of a Line y = mx + b
when
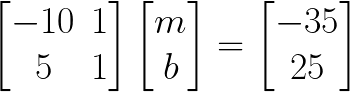
Solution to this Matrix Inverse Linear Equation practice problem is given in the video below!
Find Quadratic Equation using Matrix Inverse example question
Use Matrix Inverse to find a Quadratic Equation of a Curve y = ax2 + bx + c
when

Solution to this Matrix Inverse Quadratic Equation practice problem is given in the video below!
Minors and Cofactors example problem
Find the minors and cofactors of the following matrix.

Solution to this Linear Algebra practice problem is given in the video below!
Matrix Determinant with Arrow Technique example
Find the determinant of the following 3 x 3 matrix by using the Arrow Technique.

Solution to this Linear Algebra practice problem is given in the video below!
System Solution using Cramer’s Rule example question
Find the solution to the following system of linear equations by using Cramer’s Rule.
7x1 ![]() 2x2 = 3
2x2 = 3
3x1 + x2 = 5
Solution to this Linear Algebra practice problem is given in the video below!
Matrix Inverse using Adjoint Method example problem
Find the Inverse of the following Matrix by using the Adjoint Method.

Solution to this Linear Algebra practice problem is given in the video below!
Matrix Operations problems in Linear Algebra
Defined & Undefined Matrix Operations example question
A is a 4 x 5 matrix
B is 4 x 5 matrix
C is a 5 x 2 matrix
D is a 4 x 2 matrix
E is a 5 x 4 matrix
Compute the following matrix expressions (whenever possible):
BA =
AC + D =
AE + B =
AB + B =
E(A + B) =
E(AC) =
ET(A) =
(AT + E)D =
Solution to these Linear Algebra practice problems is given in the video below!
Matrix Operations example problem
A = 
B = 
D = 
E = 
Compute the following matrix expressions (whenever possible):
AB =
BA =
tr(4ET ![]() D) =
D) =
Solution to these Linear Algebra practice problems is given in the video below!
Gaussian & Gauss-Jordan Elimination problems in Linear Algebra
Gaussian Elimination example question
Solve the system of linear equations by using Gaussian Elimination.
x1 + 2x2 ![]() 3x3 = 6
3x3 = 6
2x1 ![]() x2 + 4x3 = 1
x2 + 4x3 = 1
x1 ![]() x2 + x3 = 3
x2 + x3 = 3
Solution to this Linear Algebra practice problem is given in the video below!
Gauss-Jordan Elimination example problem
Solve the following system of linear equations by using Gauss-Jordan Elimination.
x1 + 2x2 ![]() 3x3 = 6
3x3 = 6
2x1 ![]() x2 + 4x3 = 1
x2 + 4x3 = 1
x1 ![]() x2 + x3 = 3
x2 + x3 = 3
Solution to this Linear Algebra practice problem is given in the video below!
Linear Algebra problems (complete Playlist)
Find a variety of Linear Algebra examples and practice problems in this course.
Recent Comments