Home » Conditional Probability
Category Archives: Conditional Probability
Two-Way Table Data Probability problems
Two Way Table Data Conditional Probability example problem
When insurance companies establish policies for overing screening tests for diseases, one important factor is the value of the test predicting the disease. For example, for a certain type of disease, insurance companies may only cover the test costs if the test improves the prediction of having the disease by 80%. To help decide coverage policy for a new test, use the following data to help decide whether the test should be covered.
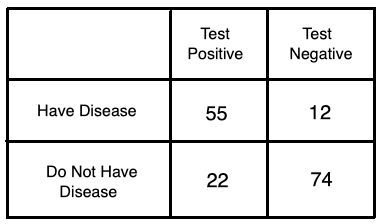
a) Find P(A) = P(Having the disease among everyone)
b) Find P(B) = P(Testing positive for everyone)
c) Find P(A and B) = P(Having the disease and testing positive)
d) Find P(A | B) = P(Having the disease given tested positive)
e) Should the test be covered? What is your conclusion? Justify your answer using the conditional probabilities above.
Solution to this Calculus Two Way Table Data Conditional Probability practice problem is given in the video below!
Venn Diagram and Conditional Probability problems
Venn Diagram Bayes Rule Probability example question
For two events we have P(A) = 0.29, P(B) = 0.43, and P(A ![]() B) = 0.65. What is P(A
B) = 0.65. What is P(A ![]() B)?
B)?
a) 0.27
b) 0.07
c) 0.16
d) 0.43
e) 0.08
f) none of the above
Solution to this Venn Diagram Probability practice problem is given in the video below!
Venn Diagram Bayes Rule Probability example problem #2
A universal set U = {1, 2, 3, 4, 5, 6, 7, 8} has subsets A = {1, 2, 3, 4} and B = {1, 2, 6, 7}. What set is A’ ![]() B?
B?
a) ![]()
b) {1, 2, 5, 6, 7, 8}
c) {1, 2, 3, 4}
d) {1, 2, 3, 4, 5, 8}
e) {1, 2}
f) none of the above
Solution to this Venn Diagram Probability practice problem is given in the video below!
Venn Diagram Probability word problem example
A manufactured component has its quality graded on its performance, appearance, and cost. Each of those three characteristics is graded as either pass or fail. There is a probability of 0.40 that a component passes on both appearance and cost. There is a probability of 0.31 that a component passes on all three characteristics. There is a probability of 0.64 that a component passes on performance. There is a probability of 0.19 that a component fails on all three characteristics. There is a probability of 0.06 that a component passes on appearance but fails on both performance and cost.
a) What is the probability that a component passes on cost but fails on both performance and appearance?
b) If a component passes on both appearance and cost, what is the probability that it passes on all three characteristics?
Solution to this Venn Diagram Probability practice problem is given in the video below!
Venn Diagram & Bayes Rule Conditional Probability example question #3
How does VENN Diagram relate to Bayes Formula

when finding Conditional Probability?
Solution to this Venn Diagram & Bayes Formula Conditional Probability practice problem is given in the video below!
Conditional Probability Bayes Rule example problem #4
On Tuesday morning, David randomly picks a microphone, and it fails. What is the probability that the microphone of brand Y was chosen, given that probability of failure for microphone X is 0.3, probability of failure for microphone Y is 0.4, probability of choosing microphone X is ![]() , and probability of choosing microphone X is
, and probability of choosing microphone X is ![]() ?
?
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
f) none of the above
Solution to this Conditional Probability Bayes practice problem is given in the video below!
Conditional Probability Bayes Rule example #5
A car brand X produces 40% of its cars at plant A and the remainder at plant B. Of all cars produced at plant A, 20% do not have a spare tire, while 30% of the cars produced at B do not have a spare tire. Car X is purchased, and it happens to have a spare tire. What is the probability that it was produced at plant B?
a) ![]()
b) ![]()
c) ![]()
d) 0.7
e) 0.8
f) none of the above
Solution to this Conditional Probability Bayes practice problem is given in the video below!
Conditional Probability Bayes Rule example question #6
David has two microphones which he uses to teach his Algebra class; one is brand X and the other is brand Y. Microphone X fails with probability 0.3, while brand Y fails with probability 0.4. On a particular morning, David picks a microphone at random. What is the probability that it will fail?
a) 0.7
b) 0.35
c) 0.12
d) 0.58
e) 0.42
f) none of the above
Solution to this Conditional Probability Bayes practice problem is given in the video below!
Recent Comments