Home » Application of Differentiation
Category Archives: Application of Differentiation
Particle Motion calculus problems
Average Velocity of a Particle example question
The velocity, in feet per second, of a particle moving along the x-axis is given by the function v(t) = et + tet. What is the average velocity of the particle from time t = 0 to time t = 3?
Solution to this Particle Motion calculus practice problem is given in the video below!
Number of Times Velocity of a Particle is Zero example problem
The position of an object attached to a spring is given by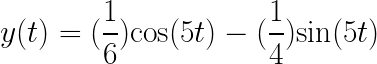 
, where t is time in seconds. In the first 4 seconds, how many times is the velocity of the object equal to 0?
Solution to this Particle Motion calculus practice problem is given in the video below!
Times When a Particle is at Rest example
A particle moves along the x-axis so that at time t ≥ 0 its position is given by 
. At what time t is the particle at rest?
Solution to this Particle Motion calculus practice problem is given in the video below!
Height of a Particle at its Maximum Upward Velocity example question
The height h, in meters, of an object at time t is given by 
. What is the height of the object at the instant when it reaches its maximum upward velocity?
Solution to this Particle Motion calculus practice problem is given in the video below!
Acceleration of a Particle at Time t example problem
A particle moves along the x-axis so that at any time t ≥ 0, its velocity is given by v(t) = 3 + 4.1cos(0.9t). What is the acceleration of the particle at time t = 4?
Solution to this Particle Motion calculus practice problem is given in the video below!
HARD Velocity Acceleration of a Particle example
At time t ≥ 0, the acceleration of a particle moving on the x-axis is a(t) = t + sin(t). At t = 0, the velocity of the particle is -2. For what value of t will the velocity of the particle be zero?
Solution to this Particle Motion calculus practice problem is given in the video below!
Maximum Acceleration of a Particle example question
Find the maximum acceleration attained on the interval 0 ≤ t ≤ 3 by the particle whose velocity is given by
Solution to this Particle Motion calculus practice problem is given in the video below!
Position of a Particle at Time t When its Velocity is First Equal To Zero example problem
A particle moves along the x-axis so that at any time t ≥ 0, its velocity is given by 
. The position of the particle is 3 at time t = 0. What is the position of the particle when its velocity is first equal to 0?
Solution to this Particle Motion calculus practice problem is given in the video below!
Specific Velocity of a Particle using its Acceleration example
A particle moves along the x-axis so that at any time t > 0, its acceleration is given by 
. If the velocity of the particle is 2 at time t = 1, find the velocity of the particle at time t = 2.
Solution to this Particle Motion calculus practice problem is given in the video below!
Time When the Particle is FARTHEST to the Right example question
A particle moves along the x-axis so that its acceleration at any time t is 
. If the initial velocity of the particle is 6, at what time t during the interval 0 ≤ t ≤ 4 is the particle farthest to the right?
Solution to this Particle Motion calculus practice problem is given in the video below!
Curve Sketching Differentiation problems
Polynomial Function Curve Sketching example question
Sketch the curve represented by the given function by finding critical values (local minimum and local maximum points) and inflection points by finding first and second Derivatives.
Solution to this Calculus Curve Sketching Differentiation practice problem is given in the video below!
Rational Function Curve Sketching example problem
Sketch the curve represented by the function below by finding critical values (local minimum and local maximum points) and inflection points by determining the first and second Derivative functions.
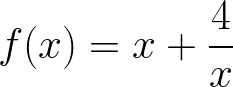
Solution to this Calculus Curve Sketching Differentiation practice problem is given in the video below!
Exponential Function Curve Sketching example
Sketch the curve represented by the given function by finding critical values (local minimum, local maximum points and general extrema) and inflection points by analyzing first and second Derivative functions.
Solution to this Calculus Curve Sketching Differentiation practice problem is given in the video below!
Related Rates calculus problems
Sphere Related Rates example problem
The radius of a sphere is r when the time is t seconds. Find the radius when the rate of change of the surface area and the rate of change of the radius are equal.
Solution to this Calculus Related Rates practice problem is given in the video below!
Balloon Related Rates example question
Gas is escaping from a spherical balloon at the rate of 4 cubic feet per minute. How fast is the surface area of the balloon shrinking when the radius of the balloon is 4 feet?
Solution to this Calculus Related Rates practice problem is given in the video below!
Approaching Cars Related Rates example
A car is traveling at 50 miles per hour due south at a point 
mile north of an intersection. A police car is traveling at 40 miles per hour due west at a point 
mile east of the same intersection. At that instant, the radar in the police car measures the rate at which the distance between the two cars is changing. What does the radar gun register?
Solution to this Calculus Related Rates practice problem is given in the video below!
Sliding Ladder Related Rates example problem
A 10-foot ladder leans against the side of the building. If the top of the ladder begins to slide down the wall at the rate of 2 feet per second, how fast is the bottom of the ladder sliding away from the wall when the top of the ladder is 8 feet off the ground?
Solution to this Calculus Related Rates practice problem is given in the video below!
Oil Spill Related Rates example question
An oil tanker has an accident and oil pours out at the rate of 150 gallons per minute. Suppose that the oil spreads onto the water in a circle at a thickness of 
inches. Given that 1 cubic inch equals 7.5 gallons, determine the rate at which the radius of the spill is increasing when the radius reaches 500 feet.
Solution to this Calculus Related Rates practice problem is given in the video below!
Trigonometry Related Rates example
A spectator at an air show is trying to follow the flight of a jet. The jet follows a straight path in front of the observer at 540 miles per hour. At its closest approach, the jet passes 600 feet in front of the person. Find the maximum rate of change of the angle between the spectator’s line of sight and a line perpendicular to the flight path, as the jet flies by.
Solution to this Calculus Related Rates practice problem is given in the video below!
Complex Trigonometry Related Rates example problem
Two buildings, of height 20 feet and 40 feet, are 60 feet apart. Suppose that the intensity of light at a point between the buildings is proportional to the angle 
in the figure. If a person is moving from right to left at 4 feet per second, at what rate is this angle changing when the person is exactly halfway between the two buildings?
Solution to this Calculus Related Rates practice problem is given in the video below!
Cone Related Rates example question
Water is running out of a conical funnel at the rate of 1 cubic inch per second. If the radius of the base of the funnel is 4 inches and the height is 8 inches, find the rate at which the water level is dropping when it is 2 inches from the top.
Solution to this Calculus Related Rates practice problem is given in the video below!
Pulley example Related Rates example
A weight W is attached to a rope 50-foot-long that passes over a pulley at a point P, 20 feet above the ground. The other end of the rope is attached to a truck at a point A, 2 feet above the ground. If the truck moves away at the rate of 9 feet per second, how fast is the weight rising when it is 6 feet above the ground?
Solution to this Calculus Related Rates practice problem is given in the video below!
Shadow Related Rates example problem
Suppose a 6-ft-tall person is x feet away from an 18-ft-tall lamppost. If the person is moving away from the lamppost at a rate of 2 feet per second, at what rate is the length of the shadow changing?
Solution to this Calculus Related Rates practice problem is given in the video below!
Kite Related Rates example question
A boy is flying a kite at a height of 150 feet. If the kite moves horizontally away from the boy at 20 feet per second, how fast is the string being paid out when the kite is 250 feet from him?
Solution to this Calculus Related Rates practice problem is given in the video below!
Curve Related Rates example
If a point moves along the curve 
,
at what point is the y-coordinate changing twice as fast as the x-coordinate?
Solution to this Calculus Related Rates practice problem is given in the video below!
Boat Related Rates example problem
A barge, whose deck is 10 feet below the level of the dock, is being drawn in by means of a cable attached to the deck and passing through a ring on the dock. When the barge is 24 feet away and approaching the dock at 
feet per second, how fast is the cable being pulled in? (Neglect any sag in the cable.)
Solution to this Calculus Related Rates practice problem is given in the video below!
HARD Related Rates Clock example question
The minute and hour hands of a clock are 15 cm and 10 cm long, respectively. Find the rates at which the angle and distance between the tips of these hands of a clock are changing when the time on the clock shows 12:30 p.m.
Solution to this Calculus Related Rates practice problem is given in the video below!
Optimization calculus problems
Inscribed Rectangle Optimization example question
Find the area of the largest rectangle that can be inscribed in a circle of radius 4.
Solution to this Calculus Optimization practice problem is given in the video below!
Rain Gutter Optimization example problem
A rain gutter is to be constructed from a metal sheet of width 30 centimeters by bending up one-third of the sheet on each side through an angle θ. How should angle θ be chosen so that the gutter will carry the maximum amount of water?
Solution to this Calculus Optimization practice problem is given in the video below!
Distance Optimization example
Find the point on the curve y = cos(x) closest to the point (0,0)
Solution to this Calculus Optimization practice problem is given in the video below!
Running Track Optimization example question
A running track is to be built around a rectangular field, with two straightaways and two semicircular curves at the ends, as indicated in the figure. The length of the track is to be 400 meters. Find the dimensions that will maximize the area of the enclosed rectangle.
Solution to this Calculus Optimization practice problem is given in the video below!
Ticket Cost Optimization example problem
Suppose that group tickets to a concert are priced at $40 per ticket if 20 tickets are ordered, up to a maximum of 50 tickets. (For example, if 22 tickets are ordered, the price is $38 per ticket). Find the number of tickets that maximizes the total cost of the tickets.
Solution to this Calculus Optimization practice problem is given in the video below!
Rectangular Ad Optimization example
An advertisement consists of a rectangular printed region plus 1-inch margins on the sides and 2-inch margins at the top and bottom. If the area of the printed region is to be 92 square inches, find the dimensions of the printed region and overall advertisement that minimize the total area.
Solution to this Calculus Optimization practice problem is given in the video below!
Soda Can Optimization example question
A soda can is to hold 12 fluid ounces. Find the dimensions that will minimize the amount of material used in its construction, assuming that the thickness of the material is uniform.
Solution to this Calculus Optimization practice problem is given in the video below!
Graph Optimization example problem
Suppose that
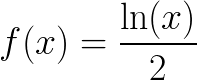
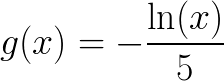
For each x in the interval (0,1), consider the rectangle formed in the following manner:
a) Its right side is the line segment connecting the points (x, f(x)) and (x, g(x))
b) Its left side lies along the y-axis
Which value of x in the interval (0,1) results in the rectangle of largest area?
Solution to this Calculus Optimization practice problem is given in the video below!
Optimization Proof example
Show that the Rectangle of Maximum Area for a given Perimeter is always a Square.
Solution to this Calculus Optimization practice problem is given in the video below!
Optimization Proof example question
Show that the Rectangle of Minimum Perimeter for a given Area is always a Square.
Solution to this Calculus Optimization practice problem is given in the video below!
Equations of Lines Tangent to Curve & Passing Point Implicit Differentiation problems
Implicit Differentiation HARD example question
Find Equations of Lines passing through the point (12, 3) and Tangent to the Curve
Solution to this Calculus Implicit Differentiation practice problem is given in the video below!
Equation of the Tangent Line Implicit Differentiation problems
Implicit Differentiation Equation of the Tangent Line example question
Find the Equation of the Tangent Line to the Curve
at the point (-1, -2)
Solution to this Calculus Implicit Differentiation practice problem is given in the video below!
Recent Comments