Home » Application of Integration
Category Archives: Application of Integration
Particle Motion calculus problems
Average Velocity of a Particle example question
The velocity, in feet per second, of a particle moving along the x-axis is given by the function v(t) = et + tet. What is the average velocity of the particle from time t = 0 to time t = 3?
Solution to this Particle Motion calculus practice problem is given in the video below!
Number of Times Velocity of a Particle is Zero example problem
The position of an object attached to a spring is given by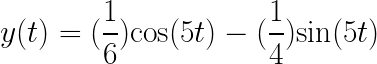 
, where t is time in seconds. In the first 4 seconds, how many times is the velocity of the object equal to 0?
Solution to this Particle Motion calculus practice problem is given in the video below!
Times When a Particle is at Rest example
A particle moves along the x-axis so that at time t ≥ 0 its position is given by 
. At what time t is the particle at rest?
Solution to this Particle Motion calculus practice problem is given in the video below!
Height of a Particle at its Maximum Upward Velocity example question
The height h, in meters, of an object at time t is given by 
. What is the height of the object at the instant when it reaches its maximum upward velocity?
Solution to this Particle Motion calculus practice problem is given in the video below!
Acceleration of a Particle at Time t example problem
A particle moves along the x-axis so that at any time t ≥ 0, its velocity is given by v(t) = 3 + 4.1cos(0.9t). What is the acceleration of the particle at time t = 4?
Solution to this Particle Motion calculus practice problem is given in the video below!
HARD Velocity Acceleration of a Particle example
At time t ≥ 0, the acceleration of a particle moving on the x-axis is a(t) = t + sin(t). At t = 0, the velocity of the particle is -2. For what value of t will the velocity of the particle be zero?
Solution to this Particle Motion calculus practice problem is given in the video below!
Maximum Acceleration of a Particle example question
Find the maximum acceleration attained on the interval 0 ≤ t ≤ 3 by the particle whose velocity is given by
Solution to this Particle Motion calculus practice problem is given in the video below!
Position of a Particle at Time t When its Velocity is First Equal To Zero example problem
A particle moves along the x-axis so that at any time t ≥ 0, its velocity is given by 
. The position of the particle is 3 at time t = 0. What is the position of the particle when its velocity is first equal to 0?
Solution to this Particle Motion calculus practice problem is given in the video below!
Specific Velocity of a Particle using its Acceleration example
A particle moves along the x-axis so that at any time t > 0, its acceleration is given by 
. If the velocity of the particle is 2 at time t = 1, find the velocity of the particle at time t = 2.
Solution to this Particle Motion calculus practice problem is given in the video below!
Time When the Particle is FARTHEST to the Right example question
A particle moves along the x-axis so that its acceleration at any time t is 
. If the initial velocity of the particle is 6, at what time t during the interval 0 ≤ t ≤ 4 is the particle farthest to the right?
Solution to this Particle Motion calculus practice problem is given in the video below!
Surface Area Integration problems
Surface Area of a Solid Integration problem example
Find the Surface Area of a solid generated by revolving the curve
, from 
to 
, about the x-axis.
Solution to this calculus Surface Area of a Solid Integration practice problem is provided in the video below!
Arc Length of a Curve Integration problems
Arc Length of a Curve Integration problem example
Find the Arc Length of a curve 
, from to 
Solution to this calculus Arc Length of a Curve Integration practice problem is provided in the video below!
Area Between Curves Integration problems
Area Between Curves Integration problem example
Find the area bounded by two curves 
and 
Solution to this calculus Area Between Curves Integration practice problem is provided in the video below!
Projectile Motion calculus problems
Projectile Motion In Two Dimensions problem example
An object is launched at angle 
from the horizontal with initial speed Vo = 98 meters per second. Determine the time of flight and the horizontal range of the projectile.
Solution to this Calculus Projectile Motion practice problem is provided in the video below!
Projectile Motion “Baseball Pitcher” example question
A baseball pitcher releases the ball horizontally from a height of 6 feet with an initial velocity of 130 feet per second. Find the height of the ball when it reaches home plate 60 feet away.
Solution to this Calculus Projectile Motion practice problem is provided in the video below!
Theoretical Projectile Motion example
Show that an object dropped from a height of H feet will hit the ground at time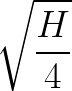 
seconds with impact velocity 
feet per second.
Solution to this Calculus Projectile Motion practice problem is provided in the video below!
Disks Washers Cylindrical Shells Volume of the Solid Integration problems
Volume of the Solid by Revolution DISK Integration Method example
Revolve the region under a curve
on the interval [0, 4] about the x-axis and find the volume of the resulting solid.
Solution to this Volume of the Solid by Rotation practice problem is provided in the video below!
Volume of the Solid by Rotation DISK Integration Method example problem
Find the volume of the solid resulting from revolving the region bounded by the lines
and 
from to 
about the y-axis.
Solution to this Volume of the Solid by Revolution practice problem is provided in the video below!
Volume of the Solid by Revolution WASHER Integration Method example question
Find the volume of the solid resulting from revolving the region bounded by lines
, and ,
about the line 
Solution to this Volume of the Solid by Rotation practice problem is provided in the video below!
Volume of the Solid by Rotation WASHER Integration Method example #2
Find the volume of the solid resulting from revolving the region bounded by lines
, and ,
about the x-axis.
Solution to this Volume of the Solid by Revolution practice problem is provided in the video below!
Volume of the Solid by Rotation CYLINDRICAL SHELL Integration Method example problem
Revolve the region bounded by the graphs of 
and 
in the first quadrant about the y-axis using Cylindrical Shells and find the volume of the resulting solid.
Solution to this Volume of the Solid by Revolution practice problem is provided in the video below!
Volume of the Solid by Revolution WASHER & SHELL Integration Method example question
Find the volume, using Washer and Cylindrical Shell methods, of the solid formed by revolving the region bounded by curves
and 
about the line 
Solution to this Volume of the Solid by Rotation practice problem is provided in the video below!
Geometric Formula PROOF Integration problems
Area of a Triangle Formula Proof example question
Use Integration techniques in order to derive the formula for the Area of a Triangle, A, such that
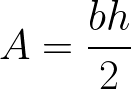
where b is the base and h is the height.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Area of a Trapezoid Formula Proof example problem
Use Integration to derive the formula for the Area of a Trapezoid, A, such that
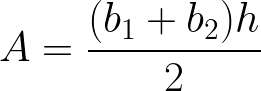
where b1 and b2 are bases and h is the height.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Area of a Circle Formula Proof example
Use Integration to derive the formula for the Area of a Circle, A, such that
where r is the radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Area of a Circle Formula Proof example question
Use Double Integration to prove the formula for the Area of a Circle, A, such that
where r is the radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Volume of a Sphere Formula Proof example problem
Use the Disk Integration method to derive the formula for the Volume of a Sphere, V, such that
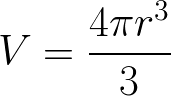
where r is the radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Volume of a Cone Formula Proof example
Use the Disk Integration method to prove the formula for the Volume of a Right Circular Cone, V, such that
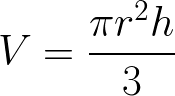
where r is the radius and h is the height.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Volume of a Torus Formula Proof example question
Use the Washer Integration method to derive the formula for the Volume of a Torus, V, such that
where r is the inner (minor) radius and R is the outer (major) radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Volume of a Torus Formula Proof example problem
Use the Shell Integration method to prove the formula for the Volume of a Torus, V, such that
where r is the inner (minor) radius and R is the outer (major) radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Surface Area of a Cone Formula Proof example
Use Integration to derive the formula for the Lateral Surface Area of a Right Circular Cone, SA, such that
where r is the radius and h is the height.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Surface Area of a Right Circular Cone Formula Proof with Double Integration example problem
Use Double Integrals to derive the formula for the Lateral Surface Area of a Right Circular Cone, SA, where
where r is the radius and h is the height.
Solution to this Calculus Geometric Formula Proof practice problem is provided in the video below!
Surface Area of a Sphere Formula Proof example question
Use Integration to prove the formula for the Surface Area of a Sphere, SA, such that
where r is the radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Volume of a Torus Formula Proof example
Use the Cylindrical Coordinates (Triple Integration) method to prove the formula for the Volume of a Torus, V, such that
where r is the inner (minor) radius and R is the outer (major) radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Volume of a Sphere Formula Proof example question
Use the Spherical Coordinates (Triple Integration) method to derive the formula for the Volume of a Sphere, V, such that
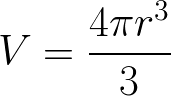
where r is the radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Volume of a Cone Formula Proof example problem
Use the Spherical Coordinates (Triple Integration) method to derive the formula for the Volume of a Right Circular Cone, V, such that
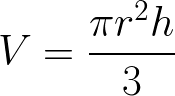
where r is the radius and h is the height.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Volume of a Torus Formula Proof example
Use the Spherical Coordinates (Triple Integration) method to prove the formula for the Volume of a Torus, V, such that
where r is the inner (minor) radius and R is the outer (major) radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Hydrostatic Force & Work problems
Work Done Stretching a Spring example question
A force of 5 pounds stretches a spring 
foot beyond its natural length. Find the work done stretching the spring 8 inches beyond its natural length.
Solution to this Calculus Work practice problem is given in the video below!
Work Done Pulling Weighty Cable/Rope example problem
We are given a fully extended cable of 150 weighing 2.00 pounds per foot. How much work is done after winding 50 feet of cable?
Solution to this Calculus Work practice problem is given in the video below!
Work Done Pulling Object by Weighty Cable example
Find the work done winding 10 feet of a 25-foot cable that weighs 4 pounds per foot when there is a 50 lb mass that hangs on the end.
Solution to this Calculus Work practice problem is given in the video below!
Work Done Pumping Liquid from a Rectangular Tank example question
A rectangular tank with a base 4 feet by 5 feet and a height of 4 feet is full of water. The water weighs 62.4 pounds per cubic foot.
a) How much work is done pumping all water out from the top of this tank?
b) How much work is done pumping only HALF of the water out from the top of this tank?
Solution to this Calculus Work practice problem is given in the video below!
Work Done Pumping Liquid from a Triangular Tank example problem
The vat shown below contains water to a depth of 2 meters. Find the work required to pump all the water to the top of the vat. (Assume the weight density of water is 9,810 Newtons per cubic meter).
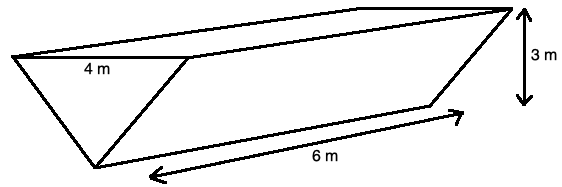
Solution to this Calculus Work practice problem is given in the video below!
Work Done Pumping Liquid from a Conical Tank example
Find the work done by pumping out molasses from a conical tank filled to 2 ft from the top of the tank. The tank has a maximum radius of 3 ft and a height of 10 ft. Molasses weighs 100 pounds per cubic foot.
Solution to this Calculus Work practice problem is given in the video below!
Work Done Pumping Liquid from a Cylindrical Tank example question
A cylindrical reservoir of diameter 4 ft and height 6 ft is half-full of water weighing 10 pounds per cubic foot. Find the work done in emptying the water over the top.
Solution to this Calculus Work practice problem is given in the video below!
Work Done Filling Spherical Tank with Water example problem
A water tower is spherical in shape with radius 50 feet, extending from 200 feet to 300 feet above ground. Compute the work done in filling the tank from the ground.
Solution to this Calculus Work practice problem is given in the video below!
Hydrostatic Force on a Dam example
A dam has the shape of a trapezoid with height 80 feet. The width at the top of the dam is 60 feet and the width at the bottom of the dam is 140 feet. Find the maximum hydrostatic force that the dam will need to withstand.
Solution to this Calculus Hydrostatic Force practice problem is given in the video below!
Hydrostatic Force on a Circular Window example question
An underwater viewing window is installed at an aquarium. The window is circular with radius 5 feet. The center of the window is 40 feet below the surface of the water. Find the hydrostatic force on the window.
Solution to this Calculus Hydrostatic Force practice problem is given in the video below!
Recent Comments