Home » Piecewise Probability Distribution Functions
Category Archives: Piecewise Probability Distribution Functions
Variance problems
Married Couples Expected Value & Variance example question
If 10 married couples are randomly seated at a round table, compute
(a) the Expected number
(b) the Variance
of the number of wives that are seated next to their husbands.
Solution to this Expected Value & Variance practice problem is given in the video below!
Expected Value problems
Expected Value example question
A box contains 8 green and 4 blue marbles. Two marbles are selected at once without replacement. What is the expected number of green marbles among the selected ones?
a) 1
b) 
c) 
d) 
e) 
f) none of the above
Solution to this Expected Value practice problem is given in the video below!
Expected Value example problem #2
You have 5 pairs of shoes. Four of them are worth $30 each, while the fifth is worth $2,000. You select a pair at random. What is the expected value of the pair you have selected?
a) $424
b) $30
c) $50.20
d) $432
e) $1,030
f) none of the above
Solution to this Expected Value practice problem is given in the video below!
Binomial Distribution Expectation example
A sample of 3 items is selected at random from a box containing 20 items of which 4 are defective. Find the expected number of defective items in the sample.
Solution to this Binomial Random Variable Expected Value practice problem is given in the video below!
Hypergeometric Distribution Expectation example question
A ball is chosen at random from each of 5 urns. Each urn contains balls as follows:
urn 1: 1 white, 5 black
urn 2: 3 white, 3 black
urn 3: 6 white, 4 black
urn 4: 2 white, 6 black
urn 5: 3 white, 7 black
Compute the expected number of white balls selected.
Solution to this Hypergeometric Random Variable Expected Value practice problem is given in the video below!
Continuous Distribution Expected Value example problem
The density function of X is given by
f(x) = { 
0 otherwise
If E[X] = 
, find the values of constants 
and 
.
Solution to this Continuous Random Variable Expected Value practice problem is given in the video below!
Independent & Identically Distributed UNIFORM Random Variables Expected Value example
If X1, X2, …, Xn are independent and identically distributed random variables having uniform distributions over (0,1),
find
E [max(X1, …, Xn)]
and
E [min(X1, …,Xn)]
Solution to this Uniform Random Variable Expected Value practice problem is given in the video below!
Continuous Distribution Random Variable problems
Continuous Distribution Probability example question
X is a continuous random variable with probability density function given by
f(x) = { 
0 otherwise
a. Find the value of C
b. What is the probability that X > 1?
Solution to this Continuous Random Variable Distribution Probability practice problem is given in the video below!
SOA Exam P CAS Exam 1 Expected Value Variance Standard Deviation probability problems
Multiple Moment Generating Functions MGF example question
A company insures homes in three cities, J, K and L. Since sufficient distance separates the cities, it is reasonable to assume that the losses occurring in these cities are independent. The moment generating functions for the loss distributions of the cities are
Let X represent the combined losses from the three cities. Calculate 
.
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
Expected Value & Probability Density Function PDF example problem
Let X be a continuous random variable with density function
{ 
Calculate the expected value of X.
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
Moment Generating Function MGF example
Let X1 , X2 , X3 be a random sample from a discrete distribution with probability function
{ 
Determine the moment generating function, M(t), of 
.
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
Expected Value & Probability Density Function PDF word problem
An insurance company’s monthly claims are modeled by a continuous, positive random variable X, whose probability density function is proportional to
Determine the company’s expected monthly claims.
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
Percentiles & Probability Density Function PDF example question
An insurer’s annual weather related loss, X, is a random variable with density function
{ 
Calculate the difference between the 30th and 70th percentiles of X.
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
Standard Deviation & Moment Generating Function MGF example problem
An actuary determines that the claim size for a certain class of accidents is a random variable, X, with a moment generating function
Determine the standard deviation of the claim size for this class of accidents.
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
Standard Deviation Table example
A probability distribution of the claim sizes for an auto insurance policy is given in the table below:
| Claim Size | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| Probability | .15 | .10 | .06 | .20 | .10 | .10 | .30 |
What percentage of the claims are within one standard deviation of the mean claim size?
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
Variance & Cumulative Distribution Function CDF example question
A random variable has the cumulative distribution function
{ 
Calculate the variance of X.
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
Variance word problem
A recent study indicates that the annual cost of maintaining and repairing a car in a town to Ontario averages 200 with a variance of 260. If a tax of 20% is introduced on all items associated with the maintenance and repair of cars (i.e., everything is made 20% more expensive), what will be the variance of the annual cost of maintaining and repairing a car?
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
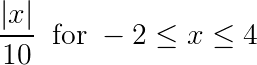
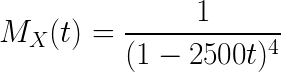
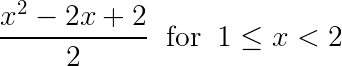
Recent Comments