Home » Volume of the Solid of Revolution
Category Archives: Volume of the Solid of Revolution
Disks Washers Cylindrical Shells Volume of the Solid Integration problems
Volume of the Solid by Revolution DISK Integration Method example
Revolve the region under a curve
![]()
on the interval [0, 4] about the x-axis and find the volume of the resulting solid.
Solution to this Volume of the Solid by Rotation practice problem is provided in the video below!
Volume of the Solid by Rotation DISK Integration Method example problem
Find the volume of the solid resulting from revolving the region bounded by the lines
![]() and
and ![]()
from ![]() to
to ![]()
about the y-axis.
Solution to this Volume of the Solid by Revolution practice problem is provided in the video below!
Volume of the Solid by Revolution WASHER Integration Method example question
Find the volume of the solid resulting from revolving the region bounded by lines
 , and
, and ![]() ,
,
about the line ![]()
Solution to this Volume of the Solid by Rotation practice problem is provided in the video below!
Volume of the Solid by Rotation WASHER Integration Method example #2
Find the volume of the solid resulting from revolving the region bounded by lines
 , and
, and ![]() ,
,
about the x-axis.
Solution to this Volume of the Solid by Revolution practice problem is provided in the video below!
Volume of the Solid by Rotation CYLINDRICAL SHELL Integration Method example problem
Revolve the region bounded by the graphs of ![]() and
and ![]() in the first quadrant about the y-axis using Cylindrical Shells and find the volume of the resulting solid.
in the first quadrant about the y-axis using Cylindrical Shells and find the volume of the resulting solid.
Solution to this Volume of the Solid by Revolution practice problem is provided in the video below!
Volume of the Solid by Revolution WASHER & SHELL Integration Method example question
Find the volume, using Washer and Cylindrical Shell methods, of the solid formed by revolving the region bounded by curves
![]() and
and ![]()
about the line ![]()
Solution to this Volume of the Solid by Rotation practice problem is provided in the video below!
Geometric Formula PROOF Integration problems
Area of a Triangle Formula Proof example question
Use Integration techniques in order to derive the formula for the Area of a Triangle, A, such that
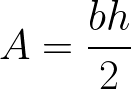
where b is the base and h is the height.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Area of a Trapezoid Formula Proof example problem
Use Integration to derive the formula for the Area of a Trapezoid, A, such that
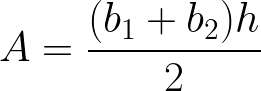
where b1 and b2 are bases and h is the height.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Area of a Circle Formula Proof example
Use Integration to derive the formula for the Area of a Circle, A, such that
![]()
where r is the radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Area of a Circle Formula Proof example question
Use Double Integration to prove the formula for the Area of a Circle, A, such that
![]()
where r is the radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Volume of a Sphere Formula Proof example problem
Use the Disk Integration method to derive the formula for the Volume of a Sphere, V, such that
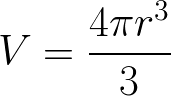
where r is the radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Volume of a Cone Formula Proof example
Use the Disk Integration method to prove the formula for the Volume of a Right Circular Cone, V, such that
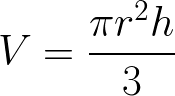
where r is the radius and h is the height.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Volume of a Torus Formula Proof example question
Use the Washer Integration method to derive the formula for the Volume of a Torus, V, such that
![]()
where r is the inner (minor) radius and R is the outer (major) radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Volume of a Torus Formula Proof example problem
Use the Shell Integration method to prove the formula for the Volume of a Torus, V, such that
![]()
where r is the inner (minor) radius and R is the outer (major) radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Surface Area of a Cone Formula Proof example
Use Integration to derive the formula for the Lateral Surface Area of a Right Circular Cone, SA, such that
![]()
where r is the radius and h is the height.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Surface Area of a Right Circular Cone Formula Proof with Double Integration example problem
Use Double Integrals to derive the formula for the Lateral Surface Area of a Right Circular Cone, SA, where
![]()
where r is the radius and h is the height.
Solution to this Calculus Geometric Formula Proof practice problem is provided in the video below!
Surface Area of a Sphere Formula Proof example question
Use Integration to prove the formula for the Surface Area of a Sphere, SA, such that
![]()
where r is the radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Volume of a Torus Formula Proof example
Use the Cylindrical Coordinates (Triple Integration) method to prove the formula for the Volume of a Torus, V, such that
![]()
where r is the inner (minor) radius and R is the outer (major) radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Volume of a Sphere Formula Proof example question
Use the Spherical Coordinates (Triple Integration) method to derive the formula for the Volume of a Sphere, V, such that
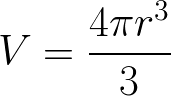
where r is the radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Volume of a Cone Formula Proof example problem
Use the Spherical Coordinates (Triple Integration) method to derive the formula for the Volume of a Right Circular Cone, V, such that
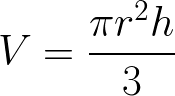
where r is the radius and h is the height.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Volume of a Torus Formula Proof example
Use the Spherical Coordinates (Triple Integration) method to prove the formula for the Volume of a Torus, V, such that
![]()
where r is the inner (minor) radius and R is the outer (major) radius.
Solution to this Calculus Geometric Formula Proof practice problem is given in the video below!
Recent Comments