Home » Geometry
Category Archives: Geometry
Angular Speed and Linear Speed problems
Converting between Angular Speed and Linear Speed example question
The angular speed ω of a point moving in a circle is defined as the quotient θ/t, where θ is the angle in radians through which the point travels in time t.
a) Find the angular speed of a point that moves through an angle of 4 radians in 6 seconds
b) Find the angular speed of a point on the rim of a wheel that travels at 60 rpm (revolutions per minute)
c) Show that the linear speed v of a point moving in a circle is related to the angular speed by the formula v = rω
d) A car is moving at the rate of 60 miles per hour, and the diameter of each wheel is 2.5 feet. Find the angular speed of the wheels.
Solution to this Angular Speed Linear Speed practice problem is provided in the video below!
Translation Geometry problems
Translation Coordinates and Graph of Translated Image example question
Find the coordinates and the translated graph of A(-2, 3), B(4, -5), and C(0, 3) by following the rule of translation:
(x, y) → (x – 5, y + 6).
Solution to this Translation Geometry practice problem is given in the video below!
Finding Coordinate RULE of Translation given Graph of Translated Image example problem
Find the coordinate rule for the translation shown in the graph below.
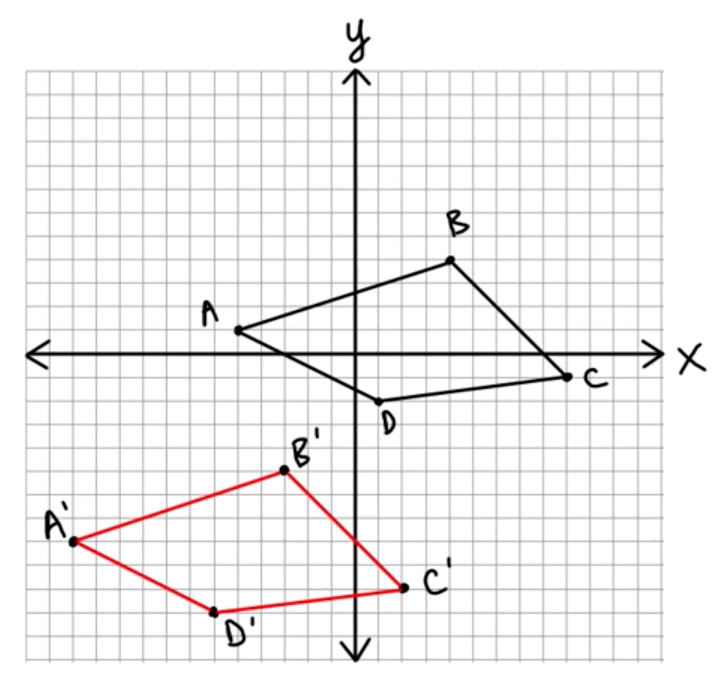
Solution to this Translation Geometry practice problem is given in the video below!
Dilation Geometry problems
Dilation Formulas and Graph with Origin the Center of Dilation example question
Graph the triangle with vertices A(-2, 4), B(1, -4), C(-3, -2) and its image after dilation by scale factor k = -3. The center of dilation is the origin.
Solution to this Dilation Geometry practice problem is given in the video below!
Dilation Formulas and Graph with Center of Dilation NOT the Origin example problem
Graph the triangle with vertices A(-2, 4), B(1, -4), C(-3, -2) and its image after dilation by scale factor k = 2. The center of dilation is the point (4, 5).
Solution to this Dilation Geometry practice problem is given in the video below!
How to Find the CENTER of DILATION COORDINATES using Given Figure and its Image problem
Find the coordinates of the center of dilation if coordinates of original figure are (-4, 14), (-10, 16), (-12, 10), (-14, 12) and coordinates of its image are (2, 1), (3, 4), (-1, 2), (4, 3).
Solution to this Dilation Geometry practice example is given in the video below!
Reflection Geometry problems
Reflection Formulas example question
Draw the image of the polygon with coordinates A(-2, 3), B(0, 2), C(3, -4), D(4, 0) by reflecting it
a) through the y-axis
b) through the x-axis
c) through the origin
d) through the line y = x
Solution to this Reflection Geometry practice problem is given in the video below!
Rotation Geometry problems
Rotation Formulas example question
a) Draw the image of the triangle with coordinates A(-6, -6), B(-6, 3), C(-2, 3) by rotating it 90 degrees clockwise
b) Draw the image of the quadrilateral with coordinates A(-3, -3), B(-1, 0), C(3, 0), D(5, -3) by rotating it 90 degrees counterclockwise
c) Draw the image of the triangle with coordinates A(-3, 2), B(1, 5), C(0, 0) by rotating it 90 degrees clockwise
d) Draw the image of the triangle with coordinates A(1, -3), B(3, 3), C(6, -3) by rotating it 180 degrees clockwise or counterclockwise
e) Draw the image of the quadrilateral with coordinates A(-5, -2), B(-4, 5), C(2, 5), D(2, 0) by rotating it 90 degrees clockwise
Solution to this Rotation Geometry practice problem is given in the video below!
Solving for x in Angles and Triangles problems
Solving for X and Y in Angles example question
Find the values of x and y using the figure below.
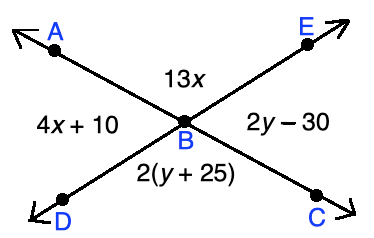
Use these values to find the following:
a) 
b) 
c) 
d) 
Solution to this value of x and y in Angles Geometry practice problem is provided in the video below!
Angles, Parallel Lines and Transversals problems
Angle Theorems Parallel Lines and Transversals example question
The following figure shows two parallel lines l and m and a transversal.
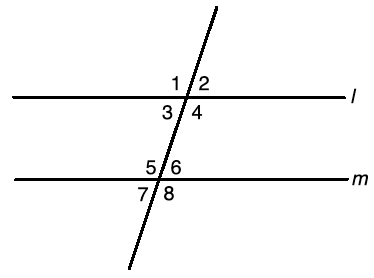
Use this figure to answer the following questions:
a) 
b) 
c) 
d) 
e) 
f) 
g) 
Solution to this Angles Parallel Lines Transversal Geometry practice problem is provided in the video below!
Angle Theorems Parallel Lines and Transversals example problem #2
Use the following figure to find the values of x and y.
Solution to this Angles Parallel Lines Transversal Geometry practice problem is provided in the video below!
Angle Theorems Parallel Lines and Transversals example #3
Use the figure below to solve for the values of x and y.
Solution to this Angles Parallel Lines Transversal Geometry practice problem is provided in the video below!
Angle Theorems Parallel Lines and Transversals example question #4
Use the given figure below to find the values of x and y.
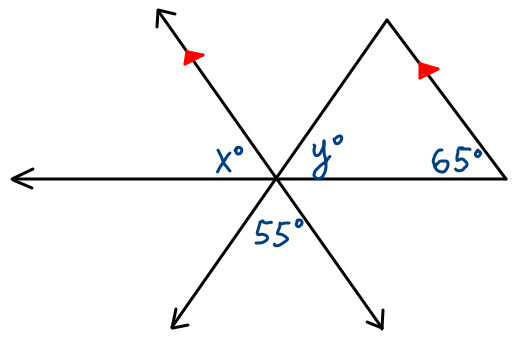
Solution to this Angles Parallel Lines Transversal Geometry practice problem is provided in the video below!
Angle Theorems Parallel Lines and Transversals example problem #5
The figure below shows a polygon with some interior angle measures provided.
Find the values of x and y.
Solution to this Angles Parallel Lines Transversal Geometry practice problem is provided in the video below!
World’s HARDEST Easy Geometry problems
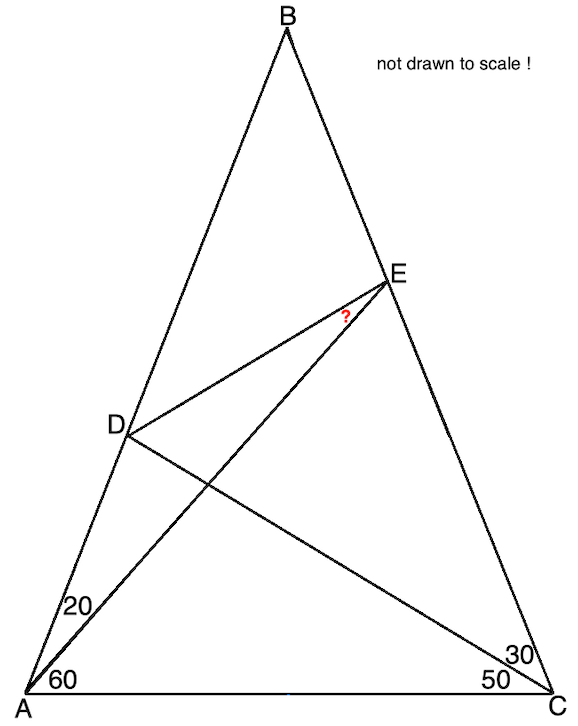
World’s HARDEST Easy Geometry problem example question
The following triangle, 
, shows angle measures in the base angles A and C, as well as line segments 
, 
and 
. Find the measure of angle AED, that is, 
.
Note: Do not use Trigonometry or Calculus to solve this problem
Solution to this World’s Hardest Easy Geometry practice problem is provided in the video below!
Orthocenter Outside the Obtuse Triangle problems
Centroid Circumcenter Incenter Orthocenter properties example question
In the following video you will learn how to find the coordinates of the Orthocenter located outside the triangle in the standard xy-plane (also known as coordinate plane or Cartesian plane). In acute and right triangles, the Orthocenter does not fall outside of the triangle. However, when the triangle in question is obtuse, that is, when one of its interior angles measures more than 90 degrees – the Orthocenter will be located outside the triangle. This is when you will need to understand the technique used to find its coordinates.
Solution to this Orthocenter in Obtuse Triangle Geometry practice problem is provided in the video below!
Centroid Circumcenter Incenter Orthocenter problems
Centroid Circumcenter Incenter Orthocenter properties example question
In this video you will learn the basic properties of triangles containing Centroid, Orthocenter, Circumcenter, and Incenter. Then you can apply these properties when solving many algebraic problems dealing with these triangle shape combinations.
Solution to this Centroid Circumcenter Incenter Orthocenter Geometry practice problem is provided in the video below!
Two Column Geometry Proof problems
Two Column Geometry Proof Intersecting Lines example problem
Given: GA = RA, AH = AT
Prove: GT is congruent to RH
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Trapezoid example
Given: AD = 8, BC = 8, and BC is congruent to CD
Prove: AD is congruent to CD
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Circle example question
Given: 
is a diameter
Prove: (CD)2 = (AD)(DB)
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Triangle example problem
Given: 
Prove: 
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Triangle example #2
Given: 
with 
the bisector of 
Prove: BFDE is a rhombus
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Circle example question #2
Given: Circle with center O and diameter
Prove: 
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Kite example problem
Given: Kite ABCD with 
E, F, G, H are midpoints of 
Prove: EFGH is a rectangle
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Triangle example #3
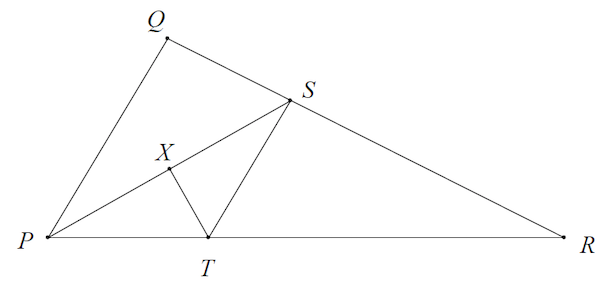
Given: 
bisects 
is a perpendicular bisector of
Prove: 
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Triangle example question #4
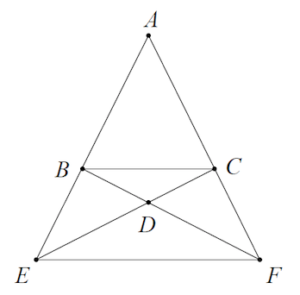
Given: is isosceles and 
Prove: 
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Parallel Lines Transversal Triangle example problem
Given: 
bisects 
bisects 
Prove: 
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Shaded Area in Geometric Figure puzzles
Shaded Area in a Square puzzle example question
In a unit square ABCD, point A is joined to the midpoint of BC, point B is joined to the midpoint of CD, point C is joined to the midpoint of DA, and point D is joined to the midpoint of AB. Find the area of the shaded region.
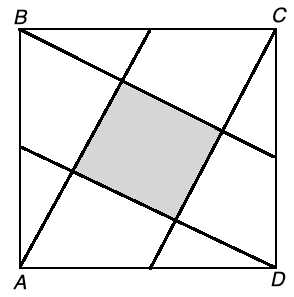
Solution to this Puzzle practice problem is given in the video below!
Shaded Area in a Square puzzle example problem
In a unit square ABCD, M is a midpoint of AD, and AC is a diagonal. Find the area of the shaded regions.
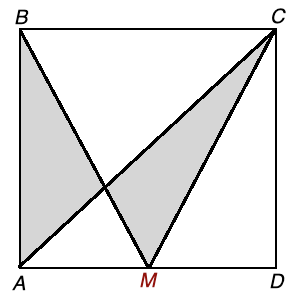
Solution to this Puzzle practice problem is given in the video below!
Shaded Area in a Square puzzle example
In the unit square ABCD, M is the midpoint and AC and BD are diagonals. Find the area of the shaded region.
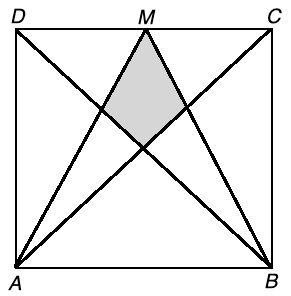
Solution to this Puzzle practice problem is given in the video below!
Shaded Area in a Square puzzle example question
In the following unit square ABCD, M is the midpoint and BD is a diagonal. Find the area of the shaded region.
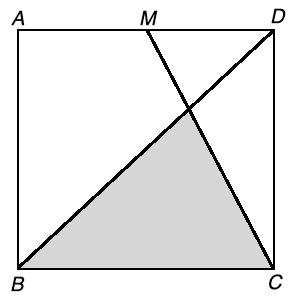
Solution to this Puzzle practice problem is given in the video below!
Shaded Area in a Square puzzle TRIGONOMETRY example problem
A square with side 1 is rotated around one vertex by an angle 
, where
and
.
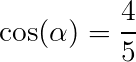Find the area of the shaded region.
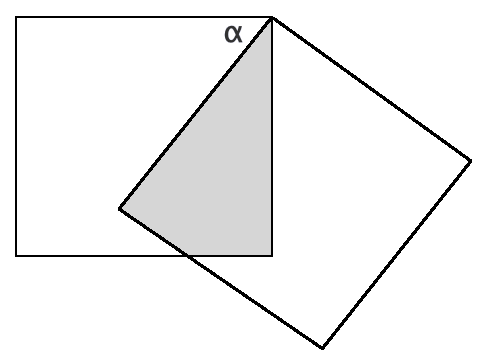
Solution to this Puzzle practice problem is given in the video below!
Shaded Area in a Rectangle puzzle example
In the following rectangle, an isosceles triangle is drawn. Find the area of the shaded region.
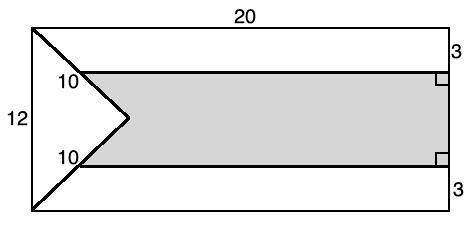
Solution to this Puzzle practice problem is given in the video below!
Shaded Area in a Rectangle puzzle example question
In the following rectangle below, find the area of the shaded region.
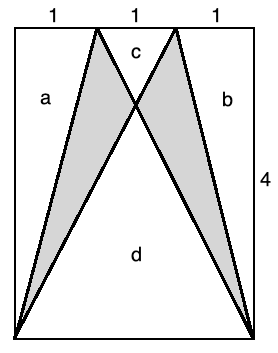
Solution to this Puzzle practice problem is given in the video below!
Geometry problems (complete Playlist)
Explore a variety of Geometry examples and practice problems applicable to K-12, Precalculus or Calculus courses.
Recent Comments