Home » Angles
Category Archives: Angles
Angular Speed and Linear Speed problems
Converting between Angular Speed and Linear Speed example question
The angular speed ω of a point moving in a circle is defined as the quotient θ/t, where θ is the angle in radians through which the point travels in time t.
a) Find the angular speed of a point that moves through an angle of 4 radians in 6 seconds
b) Find the angular speed of a point on the rim of a wheel that travels at 60 rpm (revolutions per minute)
c) Show that the linear speed v of a point moving in a circle is related to the angular speed by the formula v = rω
d) A car is moving at the rate of 60 miles per hour, and the diameter of each wheel is 2.5 feet. Find the angular speed of the wheels.
Solution to this Angular Speed Linear Speed practice problem is provided in the video below!
Trigonometric Functions WORD problems
Ferris Wheel trigonometry word problem
The Ferris wheel at Navy Pier has a diameter of 140 feet. It stands 10 feet off the ground. The wheel has 40 gondolas that seat six passengers each. It takes about 6 minutes for the Navi Pier Ferris wheel to complete one rotation.
Draw a diagram of the Navy Pier Ferris wheel and the boarding platform. Fill in the necessary information. Sketch the graph. Write a cosine equation for your curve. Write a sine equation for your curve.
Answer the following questions:
i. What is the circumference of the wheel?
ii. At what speed is the wheel traveling? Please answer in feet / second.
iii. If you begin your ride at the base of the wheel, what is the height after 1 minute? 4 minutes?
iv. At what approximate time(s) will you reach the following heights?
a) 100 ft
b) 240 ft
v. What is the length of the arc traveled by the Navy Pier Ferris wheel from the 4 o’clock to the 7 o’clock position?
Solution to this Trigonometric Function word practice problem is provided in the video below!
Roller Coaster trigonometry problem
A portion of a roller coaster is to be built in the shape of a sinusoid. You have been hired to calculate the lengths of the horizontal and vertical timber supports to be used.
a. The high and low points on the track are separated by 50 meters horizontally and 30 meters vertically. The low point is 3 meters below the ground. Letting y be the number of meters the track is above the ground and x the number of meters horizontally from the high point, write an equation expressing y in terms of x.
b. How long is the vertical timber at the high point? At x = 4 m? At x = 32 m?
c. Where does the track first go below ground?
Solution to this Trigonometric Function example practice problem is provided in the video below!
Steamboat trigonometry example word problem
Mark Twain sat on the deck of a river steamboat. As the paddlewheel turned, a point on the paddle blade moved in such a way that its distance, d, from the water’s surface was a sinusoidal function of time. When his stopwatch read 4 seconds, the point was at its highest, 16 feet above the water’s surface. The wheel’s diameter was 18 feet, and it completed a revolution every 10 seconds.
a. Sketch a graph of the sinusoid
b. Write the equation of the sinusoid
c. How far above the surface was the point when Mark’s stopwatch read:
i. 5 seconds
ii. 17 seconds
d. What is the first positive value of time at which the point was at the water’s surface? At that time, was it going into or coming out of the water? Explain.
Solution to this Trigonometric Function example word problem is provided in the video below!
Temperature trigonometry word problem
The max temperature in Buenos Aires is on January 15 and is 33 degrees Celsius. The minimum temperature is on July 16 (day 197) and is 9 degrees Celsius. (Assume the period is 365 days).
a) Sketch the temperature as a function of time
b) Find the equation for the temperature, T, as a function of time, t.
c) What is the temperature on Mother’s Day, May 10?
d) Give the dates during a one year period when the temperature is below 18 degrees Celsius.
Solution to this Trigonometric Function example word problem is provided in the video below!
Rotation Geometry problems
Rotation Formulas example question
a) Draw the image of the triangle with coordinates A(-6, -6), B(-6, 3), C(-2, 3) by rotating it 90 degrees clockwise
b) Draw the image of the quadrilateral with coordinates A(-3, -3), B(-1, 0), C(3, 0), D(5, -3) by rotating it 90 degrees counterclockwise
c) Draw the image of the triangle with coordinates A(-3, 2), B(1, 5), C(0, 0) by rotating it 90 degrees clockwise
d) Draw the image of the triangle with coordinates A(1, -3), B(3, 3), C(6, -3) by rotating it 180 degrees clockwise or counterclockwise
e) Draw the image of the quadrilateral with coordinates A(-5, -2), B(-4, 5), C(2, 5), D(2, 0) by rotating it 90 degrees clockwise
Solution to this Rotation Geometry practice problem is given in the video below!
Solving for x in Angles and Triangles problems
Solving for X and Y in Angles example question
Find the values of x and y using the figure below.
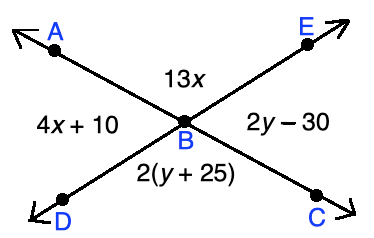
Use these values to find the following:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Solution to this value of x and y in Angles Geometry practice problem is provided in the video below!
Angles, Parallel Lines and Transversals problems
Angle Theorems Parallel Lines and Transversals example question
The following figure shows two parallel lines l and m and a transversal.
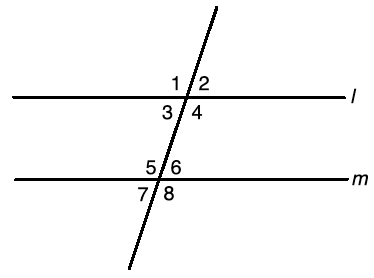
Use this figure to answer the following questions:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
f) ![]()
g) ![]()
Solution to this Angles Parallel Lines Transversal Geometry practice problem is provided in the video below!
Angle Theorems Parallel Lines and Transversals example problem #2
Use the following figure to find the values of x and y.

Solution to this Angles Parallel Lines Transversal Geometry practice problem is provided in the video below!
Angle Theorems Parallel Lines and Transversals example #3
Use the figure below to solve for the values of x and y.

Solution to this Angles Parallel Lines Transversal Geometry practice problem is provided in the video below!
Angle Theorems Parallel Lines and Transversals example question #4
Use the given figure below to find the values of x and y.
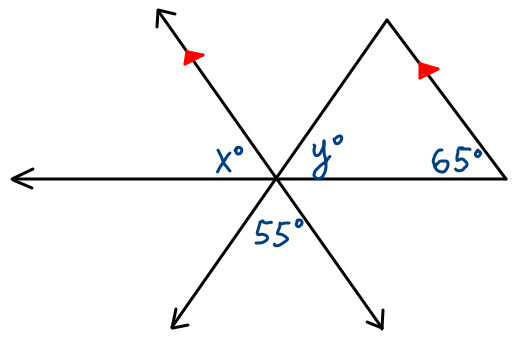
Solution to this Angles Parallel Lines Transversal Geometry practice problem is provided in the video below!
Angle Theorems Parallel Lines and Transversals example problem #5
The figure below shows a polygon with some interior angle measures provided.

Find the values of x and y.
Solution to this Angles Parallel Lines Transversal Geometry practice problem is provided in the video below!
Rotation of Axes problems
Angle of Rotation of Axes problem example
Find an appropriate angle through which to rotate axes to eliminate the xy term in the equation
![]()
Solution to this Rotation of Axes practice problem is provided in the video below!
COORDINATE Equations of Rotation of Axes example question
Find the Transformation Equations to rotate axes through an appropriate angle to eliminate the xy term in the equation
![]()
Solution to this Rotation of Axes practice problem is provided in the video below!
New Axes of Rotation EQUATION example
Find the Equation into which
![]()
is transformed when there is rotation of the axes through an appropriate angle to eliminate the xy term in the given equation.
Solution to this Rotation of Axes practice problem is provided in the video below!
Vector word problems
Horizontal and Vertical Components of a Force Vector problem example
A force of 46.3 pounds is applied at an angle of 34.8º to the horizontal. Resolve the force into horizontal and vertical components.
Solution to this Horizontal Vertical Components of a Force Vector word practice problem is provided in the video below!
HARD Parallel Perpendicular Weight Vector Components to Surface word problem
A weight of 75 pounds is resting on a surface inclined at an angle of 25º to the ground. Find the components of the weight parallel and perpendicular to the surface.
Solution to this Parallel Perpendicular Weight Vector Components word practice problem is provided in the video below!
VERY HARD Resultant Force Vector example question
Find the resultant of two forces, one with magnitude 155 pounds and direction N50ºW, and a second with magnitude 305 pounds and direction S55ºW.
Solution to this Resultant Force Vector word practice problem is provided in the video below!
Plane Wind vector example problem
An airplane has an airspeed of 430 miles per hour at a bearing of E45ºS (45 degrees South of East). The wind velocity is 35 miles per hour in the direction of N30ºE (30 degrees East of North). Find the ground speed and true course of the plane using vectors.
Solution to this Plane Wind vector word practice problem is provided in the video below!
Law of Cosines problems
Law of Cosines word problem example
Two sides of a parallelogram are 9 and 15 units in length. The length of the shorter diagonal of the parallelogram is 14 units. Find the length of the long diagonal.
Solution to this Law of Cosines word practice problem is provided in the video below!
HARD Law of Cosines word problem
A new car leaves an auto transport trailer for a test drive in the flat surface desert in the direction N47ºW at constant speed of 65 miles per hour. The trailer proceeds at constant rate of 50 miles per hour due East. If the car has enough fuel for exactly 3 hours of riding at constant speed, what is the maximum distance in the same direction that the car can cover in order to safely return to the trailer?
Solution to this Law of Cosines word practice problem is provided in the video below!
Law of Sines problems
Law of Sines word problem example
A radio antenna is attached to the top of the building. From a point 12.5 meters from the base of the building, on level ground, the angle of elevation of the bottom of the antenna is 47.2 degrees and the angle of elevation of the top is 51.8 degrees. Find the height of the antenna.
Solution to this Law of Sines word practice problem is provided in the video below!
Law of Sines Triangle Area PROOF problem
Show that for any triangle the area is one-half the product of any two sides and sine of the angle formed between these sides. That is,

Solution to this Law of Sines Triangle Area PROOF practice problem is provided in the video below!
Inverse Trigonometric Functions problems
Hard Inverse Trigonometric Expression Value example question
Evaluate the following Trigonometric Expression:
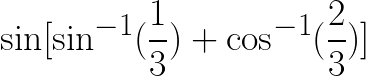
Solution to this Inverse Trigonometric Expression Value practice problem is provided in the video below!
Rectangle Word Problem with ArcTangent example
A rectangle is 173 meters long and 106 meters high. Find the angle between diagonal and the longer side.
Solution to this Inverse Trigonometric Function word practice problem is provided in the video below!
Trigonometric Equations with Angle Sum, Difference, Multiple, Half-Angle Formulas problems
Trigonometric Equation Double-Angle and Product-To-Sum example
Solve the following Trigonometric Equations using Double-Angle and Product-To-Sum formulas:
sin2θ – sinθ = 0
cosx + cos3x = cos2x
Solution to this Trigonometric Equation Double-Angle Product-To-Sum practice problem is provided in the video below!
Trigonometric Angle Sum, Difference, Multiple, Half-Angle Formulas problems
Trigonometric Angle Sum and Difference example question
Find the value of the following Trigonometric Expressions using Angle Sum or Difference formulas:
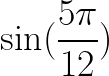
cos(105º)
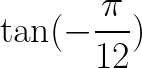
Solution to this Trigonometric Angle Sum Difference practice problem is provided in the video below!
Trigonometric Equations problems
Solution to Trigonometric Equation example question
Solve the following Trigonometric Equations:
![]()
tan(3t) = 1
2cos2u = cosu
![]()
ln(sinx) = 0
Solution to this Trigonometric Equations practice problem is provided in the video below!
Conversion of Radians, Degrees, Minutes, and Seconds problems
Radian Degree Minute Second Transformation example question
a) Convert the following angle measure given in Radians into Degrees, Minutes and Seconds:
5 Radians
b) Convert the following angle measure in Degrees, Minute and Seconds into Radians:
424o34‘ 24”
Solution to this Angle Measure Radian Degree Minutes Seconds Conversion practice problem is provided in the video below!
Graphing Trigonometric Functions problems
Amplitude Period Phase Shift of Trigonometric Functions example
Find the Amplitude, Period, Phase Shift, and Vertical Shift for each of the following Trigonometric Functions:
![]()
![]()
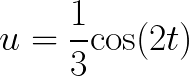
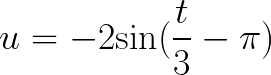
Solution to this Trigonometric Function Graph practice problem is provided in the video below!
All Key Features of Trigonometric Functions example problem
For each of the following Trigonometric Functions, find the Amplitude, Period, Frequency, Midline Equation, Phase Shift, Vertical Shift, Horizontal Stretch or Shrink, Vertical Stretch or Shrink, Domain, and Range.
![]()
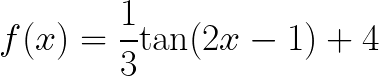
Solution to this Trigonometric Function Graph practice problem is provided in the video below!
GRAPH of Trigonometric Functions example question
Draw a Graph of the following Trigonometric Functions:
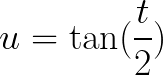
![]()
Solution to this Graph of Trigonometric Function practice problem is provided in the video below!
Basic Trigonometric Angles and Values problems
Find ANY Known Trigonometric Value by Hand example question
How do you find the values like 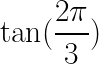 or
or 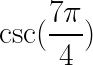 or
or 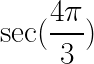 ?
?
There is a way to use the Unit Circle information and fill out your own Table of Values fast!
All you need is to start with sine function values in the interval [0, ![]() ]
]
Watch the video below with a detailed tutorial and start being a pro at this!
Solution to this Basic Trigonometric Function Values practice problem is provided in the video below!
Reference Angles problems
Finding Trigonometric Values Using Reference Angles example question
Find the value of the following Trigonometric Expressions using appropriate Reference Angles:
a) sin(120º)
b) 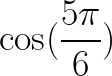
c) tan(-45º)
d) 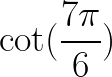
e) sec(240º)
f) 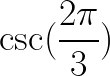
Solution to this Reference Angle practice problem is provided in the video below!
Trigonometric Functions problems
Find All Six Trigonometric Functions using Rectangular Coordinates or given Angle example question
a) If t is a point on the unit circle with coordinates 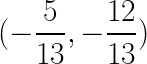 , find the six Trigonometric Functions of t
, find the six Trigonometric Functions of t
b) Find the six Trigonometric Functions of ![]()
Solution to this Trigonometric Function practice problem is provided in the video below!
World’s HARDEST Easy Geometry problems
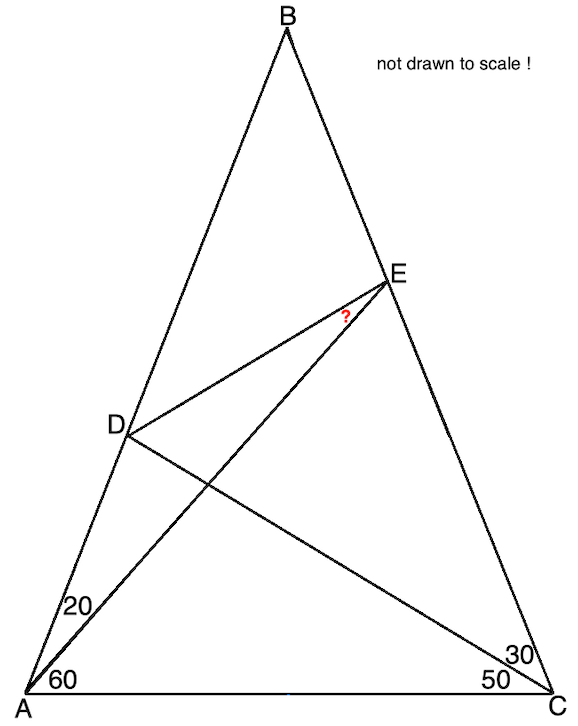
World’s HARDEST Easy Geometry problem example question
The following triangle, ![]() , shows angle measures in the base angles A and C, as well as line segments
, shows angle measures in the base angles A and C, as well as line segments ![]() ,
, ![]() and
and ![]() . Find the measure of angle AED, that is,
. Find the measure of angle AED, that is, ![]() .
.
Note: Do not use Trigonometry or Calculus to solve this problem
Solution to this World’s Hardest Easy Geometry practice problem is provided in the video below!
Orthocenter Outside the Obtuse Triangle problems
Centroid Circumcenter Incenter Orthocenter properties example question
In the following video you will learn how to find the coordinates of the Orthocenter located outside the triangle in the standard xy-plane (also known as coordinate plane or Cartesian plane). In acute and right triangles, the Orthocenter does not fall outside of the triangle. However, when the triangle in question is obtuse, that is, when one of its interior angles measures more than 90 degrees – the Orthocenter will be located outside the triangle. This is when you will need to understand the technique used to find its coordinates.
Solution to this Orthocenter in Obtuse Triangle Geometry practice problem is provided in the video below!
Centroid Circumcenter Incenter Orthocenter problems
Centroid Circumcenter Incenter Orthocenter properties example question
In this video you will learn the basic properties of triangles containing Centroid, Orthocenter, Circumcenter, and Incenter. Then you can apply these properties when solving many algebraic problems dealing with these triangle shape combinations.
Solution to this Centroid Circumcenter Incenter Orthocenter Geometry practice problem is provided in the video below!
Two Column Geometry Proof problems
Two Column Geometry Proof Intersecting Lines example problem

Given: GA = RA, AH = AT
Prove: GT is congruent to RH
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Trapezoid example

Given: AD = 8, BC = 8, and BC is congruent to CD
Prove: AD is congruent to CD
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Circle example question

Given: ![]() is a diameter
is a diameter
![]()
Prove: (CD)2 = (AD)(DB)
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Triangle example problem

Given: ![]()
Prove: ![]()
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Triangle example #2

Given: ![]() with
with ![]() the bisector of
the bisector of ![]()
![]()
Prove: BFDE is a rhombus
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Circle example question #2

Given: Circle with center O and diameter ![]()
![]()
Prove: ![]()
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Kite example problem

Given: Kite ABCD with ![]()
E, F, G, H are midpoints of ![]()
Prove: EFGH is a rectangle
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Triangle example #3
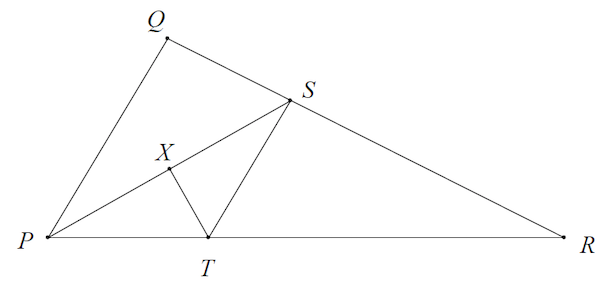
Given: ![]() bisects
bisects ![]()
![]() is a perpendicular bisector of
is a perpendicular bisector of ![]()
Prove: ![]()
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Triangle example question #4
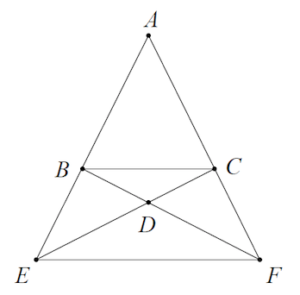
Given: ![]() is isosceles and
is isosceles and ![]()
Prove: ![]()
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Two Column Geometry Proof Parallel Lines Transversal Triangle example problem

Given: ![]()
![]() bisects
bisects ![]()
![]() bisects
bisects ![]()
Prove: ![]()
Solution to this Two Column Geometric Proof practice problem is given in the video below!
Shaded Area in Geometric Figure puzzles
Shaded Area in a Square puzzle example question
In a unit square ABCD, point A is joined to the midpoint of BC, point B is joined to the midpoint of CD, point C is joined to the midpoint of DA, and point D is joined to the midpoint of AB. Find the area of the shaded region.
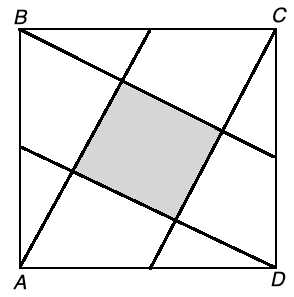
Solution to this Puzzle practice problem is given in the video below!
Shaded Area in a Square puzzle example problem
In a unit square ABCD, M is a midpoint of AD, and AC is a diagonal. Find the area of the shaded regions.
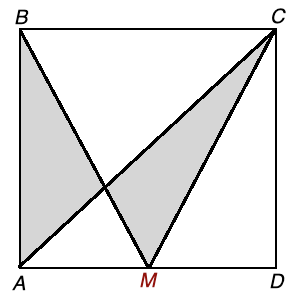
Solution to this Puzzle practice problem is given in the video below!
Shaded Area in a Square puzzle example
In the unit square ABCD, M is the midpoint and AC and BD are diagonals. Find the area of the shaded region.
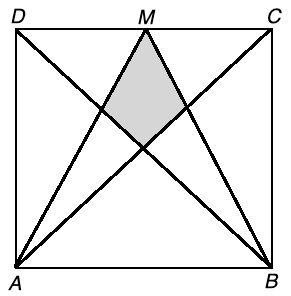
Solution to this Puzzle practice problem is given in the video below!
Shaded Area in a Square puzzle example question
In the following unit square ABCD, M is the midpoint and BD is a diagonal. Find the area of the shaded region.
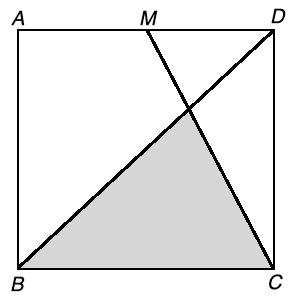
Solution to this Puzzle practice problem is given in the video below!
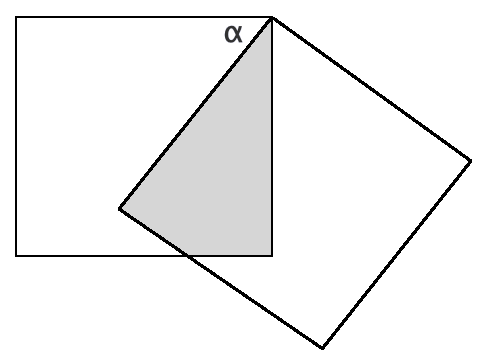
Shaded Area in a Square puzzle TRIGONOMETRY example problem
A square with side 1 is rotated around one vertex by an angle ![]() , where
, where
![]()
and
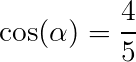 .
.
Find the area of the shaded region.
Solution to this Puzzle practice problem is given in the video below!
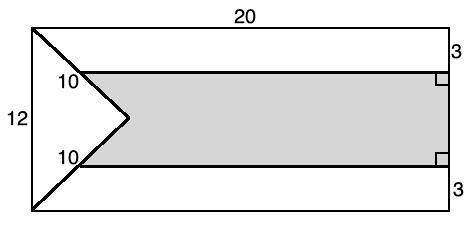
Shaded Area in a Rectangle puzzle example
In the following rectangle, an isosceles triangle is drawn. Find the area of the shaded region.
Solution to this Puzzle practice problem is given in the video below!
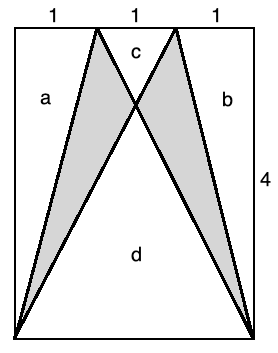
Shaded Area in a Rectangle puzzle example question
In the following rectangle below, find the area of the shaded region.
Solution to this Puzzle practice problem is given in the video below!
Geometric Formula as a Function problems
Perimeter as a Function of Area example question
a. Express the area, A , of an equilateral triangle as a function of one side S .
b. Express the perimeter, P , of the triangle as a function of the area A .
Solution to this Geometric Functions practice problem is given in the video below!
Polar Coordinates problems
Polar Rectangular Coordinates Conversion example question
Convert the following Rectangular coordinates to Polar coordinates:
a. (2, -2)
b. (0, 3)
c. (3, 4)
Solution to this Polar Coordinates practice problem is given in the video below!
Rectangular Polar Coordinates Conversion example problem
Convert the following Polar coordinates to Rectangular coordinates:
a. 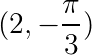
b. (0, 3)
c. 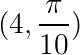
Solution to this Polar Coordinates practice problem is given in the video below!
Rectangular Polar Coordinates Conversion example
Convert the following Polar coordinates to Rectangular coordinates:
a. ![]()
b. ![]()
c. ![]()
Solution to this Polar Coordinates practice problem is given in the video below!
Rectangular Equation & Polar Equation Conversion example question
Find Polar Equations from Rectangular Equation
![]()
Solution to this Polar Coordinates practice problem is given in the video below!
Polar Equations Sketch & X–Y Equation Conversion example problem
Sketch the given Polar Equations and find their corresponding X–Y Equation:
a. r = 4
b. 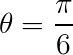
c. ![]()
d. ![]()
Solution to this Polar Coordinates practice problem is given in the video below!
Hard Polar Equations Sketch example
Sketch the given Polar Equations:
![]()
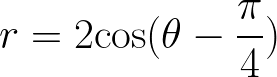
Solution to this Polar Coordinates practice problem is given in the video below!
Parametric Equation problems
Parametric Equation Sketch & X–Y Equation Conversion example question
Sketch the given Parametric Equation and find its corresponding X–Y Equation:
![]()
![]()
Solution to this Parametric Equations & Curves practice problem is given in the video below!
Parametric Equation Sketch & X–Y Equation Conversion example problem
Sketch the given Parametric Equation and find its equivalent X–Y Equation:
![]()
![]()
Solution to this Parametric Equations & Curves practice problem is given in the video below!
Parametric Equation Sketch & X–Y Equation Conversion example
Find Parametric Equations from the given X–Y equation:
Circle with radius 3, centered at (2, 1) and drawn counterclockwise.
Solution to this Parametric Equations & Curves practice problem is given in the video below!
Parametric Equation Sketch & X–Y Equation Conversion example question
Derive Parametric Equations from the given X–Y equation:
Line from (-2, 4) to (6, 1).
Solution to this Parametric Equations & Curves practice problem is given in the video below!
Parametric Equation Sketch & X–Y Equation Conversion example problem
Find Parametric Equations by using the given X–Y equation:
![]()
from (2, -2) to (0, 2).
Solution to this Parametric Equations & Curves practice problem is given in the video below!
Parametric Equations: Points of Intersection of Two Curves example
Find the coordinates of the points of Intersection of two given Parametric Curves:
![]()
![]()
Solution to this Parametric Equations & Curves practice problem is given in the video below!
Parametric Equations of a PROJECTILE example problem
A projectile is fired at an angle of inclination α, with 0 < α < π/2, at an initial speed of vo. Parametric equations for its path can be shown to be x = votcos(α), y = votsin(α) – (gt ²)/2, with t representing time.
a) Eliminate the t parameter and find the value of t when the projectile hits the ground.
b) Sketch the path of the projectile for the case α = π/6, vo = 32 ft/sec, g = 32 ft/sec ².
Solution to this Parametric Equations of a Projectile practice problem is given in the video below!
Parametric Equations: Object Position, Velocity & Speed example question
Find the Position, Velocity and Speed of an Object by using the following Parametric Equation:
![]()
![]()
Solution to this Parametric Equations & Curves practice problem is given in the video below!
Slope of the Parametric Curve example problem
Find the Slope of the Tangent Line to the Curve
![]()
![]()
Solution to this Parametric Equations & Curves practice problem is given in the video below!
Parametric Curves: Coordinates of the Points of Vertical & Horizontal Tangent Lines example
Find the Coordinates of the Points of Vertical and Horizontal Tangent Lines to the Curve
![]()
![]()
Solution to this Parametric Equations & Curves practice problem is given in the video below!
Parametric Curves: Arc Length example question
Find the Arc Length of a Parametric Curve
![]()
![]()
Solution to this Parametric Equations & Curves practice problem is given in the video below!
Parametric Curves: Area example problem
Find the Area enclosed by a Parametric Curve
![]()
![]()
in the interval
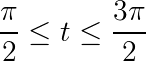
Solution to this Parametric Equations & Curves practice problem is given in the video below!
Conic Section Proof problems
Parabola Directrix Conic Section Proof example question
Show that in polar coordinates the equation of a conic section with (one) focus at the pole and directrix,
the line
![]()
can be written as
 .
.
Solution to this Conic Section Proof practice problem is given in the video below!
Trigonometric Identity Proof problems
Trigonometric Identity Proofs example problem #1
Show that
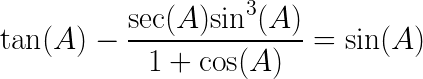
Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proof example question #2
Show that the following equation is valid.
![]()
Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proofs example #3
Prove the validity of the following equation.
![]()
Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proof example problem #4
Prove that
![]()
Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proofs example question #5
Prove the following identity.

Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proof example #6
Show that the following identity holds.
![]()
Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proofs example problem #7
Prove the following identity.

Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proof example question #8
Verify the given identity.

Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proofs example #9
Show that the identity given below is valid.

Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proof example problem #10
Verify the given three Trigonometric Identities:
(a)

(b)
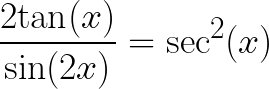
(c)

Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proof example question #11
Show that the following Trigonometric Identity is true:

Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proof example question #12
Verify that the following Trigonometric Identities hold:
a. sin(-x) = -sin(x)
b. ![]()
c. 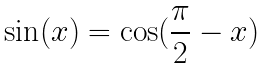
d. sin(2x) = 2sin(x)cos(x)
e. ![]()
f. cos(-x) = cos(x)
g. ![]()
Solution to this Trigonometric Identity Proof practice example question is given in the video below!
Recent Comments