Compound Interest problems
Compound Interest example problem
Suppose you make a deposit of $8,000 in the bank account that earns you 5.5% interest. Assuming that you are not withdrawing any funds, find the amount, in dollars, that will be in your bank account 1 year from the date of your initial deposit if
a) Interest is compounded daily
b) Interest is compounded monthly
c) Interest is compounded quarterly
d) Interest is compounded continuously
Solution to this Compound Interest practice problem is given in the video below!
TRY IT YOURSELF example question
On January 1, 2021 you borrow a $15,000 loan from the bank with a 7.5% accrued interest. If you do not plan on making any payments during the loan period, find the total balance of your loan, in dollars, that you will owe to the bank on January 1, 2022 for
a) Daily compounded interest
b) Weekly compounded interest
c) Monthly compounded interest
d) Quarterly compounded interest
e) Semi-annually compounded interest
f) Continuously compounded interest
Function Domain and Range problems
Finding Domain of a Function example problem
Find the domain of the following functions and use number line to show finite solution:
![]()
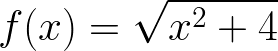


Solution to this Function Domain practice problem is given in the video below!
Finding Range of a Function example question
Find the range of the following functions and use the xy-plane to draw the solution set:
![]()
![]()
Solution to this Function Range practice problem is given in the video below!
Find SQUARE ROOT Function Given Domain, Range, and Rate of Change example
Find the Square Root Function given the following information:
Increasing: ![]()
Range: ![]()
Rate of Change over interval ![]() is 4.
is 4.
Solution to this Square Root Function practice problem is given in the video below!
Equation from Table of Ordered Pairs problems
Linear Quadratic Exponential Equation Comparison from Table of Ordered Pairs example question
Determine whether the given set of ordered pairs (x, y) below follows a Linear, Quadratic or Exponential Equation such as
![]()
![]()
![]()
Then, find the missing constants in that Equation.
(x, y)
(3, 81)
(4, 144)
(5, 225)
(6, 324)
(7, 441)
Solution to this Table of Values Linear Quadratic Exponential Equation practice problem is given in the video below!
Linear Quadratic Exponential Equation Comparison from Table of Ordered Pairs example problem
Given the set of ordered pairs (x, y) below determine whether the Graph shows a Linear, Quadratic or Exponential Equation such as
![]()
![]()
![]()
Then, find the missing constants in that Equation.
(x, y)
(1, -3)
(2, -9)
(3, -27)
(5, -243)
Solution to this Table of Values Linear Quadratic Exponential Equation practice problem is given in the video below!
Tree Diagram Probability problems
Tree Diagram Spinner example problem
A fair spinner showing numbers 1 through 3 of equal area is spun twice. Find the probabilities of the following events:
a) The sum of numbers landed on is odd
b) The sum of numbers landed on is even
c) The two numbers are different
d) Given even first number, the second number is even
e) Given odd first number, the second number is odd
f) The product of the two numbers landed on is less than 6
Solution to this Calculus Tree Diagram Probability practice problem is given in the video below!
Tree Diagram Conditional Probability example question #2
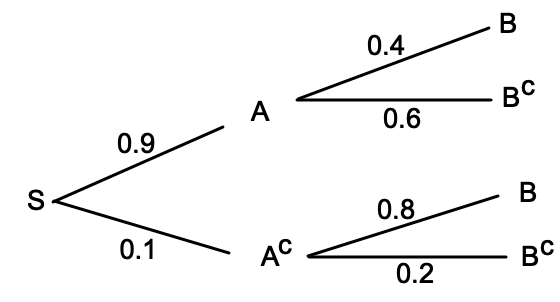
For the given Tree Diagram, calculate the P(A | Bc).
Solution to this Calculus Tree Diagram Probability practice problem is given in the video below!
Tree Diagram Marbles in a Jar probability example
Suppose we have 3 jars: A, B and C. Jar A contains 2 red marbles and 1 blue marble. Jar B contains 1 red marble and 2 blue marbles. Jar C contains 2 red marbles and 2 blue marbles. We select a jar at random. The probability we select A is ![]() . The probability we select B is
. The probability we select B is ![]() . The probability we select C is
. The probability we select C is ![]() . From the selected jar, we choose 1 marble; all marbles in the jar have the same chance of being selected.
. From the selected jar, we choose 1 marble; all marbles in the jar have the same chance of being selected.
a) What is the probability the chosen marble is red?
b) Given that the chosen marble is red, what is the probability that the selected jar was A?
Solution to this Calculus Tree Diagram Probability practice problem is given in the video below!
Tree Diagram HARD Steroid Drug probability example problem
In recent years, the “Tour de France” cycling race has been plagued with accusations that cyclists have taken steroids to boost their performance. Testing for these steroids has been difficult. The level of steroids that naturally occur in the human body can vary between individuals and the levels can change throughout the day. Testing for the presence of steroids is expensive and time-consuming. Racers are randomly chosen for drug tests. Suppose that 2% of racers have taken an illegal steroid. Assume that if they took the drug, there is a 99% chance that the test will return a “positive” reading and the athlete will be disqualified.
a) Draw a Tree Diagram showing the probabilities for the sequence of events in which an athlete either takes or does not take a drug, and then is tested for the presence of the drug.
b) What is the probability that a randomly chosen cyclist will be steroid-free and will still test positive for steroids?
c) What is the probability that a randomly chosen cyclist will be disqualified due to a “positive” reading?
Solution to this Calculus Tree Diagram Probability practice problem is given in the video below!
Differentials problems
Total Differential example word problem
Use Differentials to estimate the amount of tin in a closed tin can with diameter 8 cm and height 12 cm if the tin is 0.04 cm thick.
Solution to this Calculus Differentials practice problem is given in the video below!
Tangent Plane problems
Equation of the Plane Tangent to Surface example problem
Find an equation of the tangent plane to the given surface at the specified point:
Surface z = 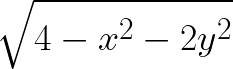
Point (1, -1, 1)
Solution to this Calculus Tangent Plane practice problem is given in the video below!
Business Calculus Optimization problems
Demand Revenue Optimization example problem
A store has been selling 200 DVD burners a week at $350 each. A market survey indicates that for each $10 rebate offered to buyers, the number of units sold will increase by 20 a week. Find the demand function and the revenue function. How large a rebate should the store offer to maximize its revenue?
Solution to this Business Calculus Optimization practice problem is given in the video below!
Algebra Work word problems
Printing Job word problem example
Jack can complete a printing job alone in 12 hours. With Jack’s help, Susan can complete this job in 8 hours. How long would it take her to complete this job alone?
Solution to this Algebra Work word practice problem is given in the video below!
Binomial Distribution Normal Approximation problems
Normal Approximation for Binomial Random Variable example problem
The median age of residents of the United States is 37.2 years. If a survey of 200 residents is taken, approximate the probability that at least 110 will be under 37.2 years of age.
Solution to this probability Binomial Distribution Normal Approximation practice problem is given in the video below!
Binomial Random Variable Normal Approximation HARD example question
The weekly amount sent by a small company for in-state travel has approximately a normal distribution with mean $1450 and standard deviation $220.
(a) What is the probability that the actual expenses will exceed $1560 in 20 or more weeks during the next year?
(b) What is the probability that the actual expenses would exceed $1500 for between 18 and 24 weeks, inclusive during the next year?
Solution to this probability Binomial Distribution Normal Approximation problem is given in the video below!
Double Improper Integral problems
DOUBLE Improper Integral example problem
Investigate convergence or divergence of the Double Improper Integral provided below.

Solution to this Calculus Double Improper Integrals practice problem is given in the video below!
Recent Comments