Combined Variation and Proportion problems
Combined Variation and Proportion example question
If z varies directly as the square root of x and inversely as y, and z = 5 when x = 3 and y = 12, find z when x = 27 and y = 5.
Solution to this Combined Variation and Proportion practice problem is provided in the video below!
Joint Variation and Proportion problems
Joint Variation and Proportion example question
If z varies jointly as x and y, and z = 3 when x = 4 and y = 6, find z when x = 20 and y = 9.
Solution to this Joint Variation and Proportion practice problem is provided in the video below!
Inverse Variation and Proportion problems
Inverse Variation and Proportion example question
If y varies inversely as the square root of x, and y = 2 when x = 
, find y when x = 2.
Solution to this Inverse Variation and Proportion practice problem is provided in the video below!
Direct Variation and Proportion problems
Direct Variation and Proportion example question
If y varies directly as the fourth power of x, and y = 2 when x = , find y when x = 2.
Solution to this Direct Variation and Proportion practice problem is provided in the video below!
Composite Functions problems
Hard Composite Functions example question
Using the four given functions
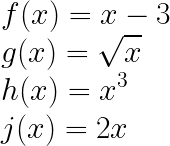
Express the following Functions in Composite form:
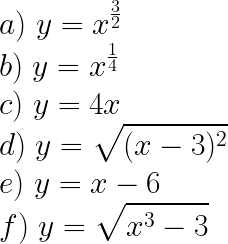
Solution to this Composite Functions practice problem is provided in the video below!
Angles, Parallel Lines and Transversals problems
Angle Theorems Parallel Lines and Transversals example question
The following figure shows two parallel lines l and m and a transversal.
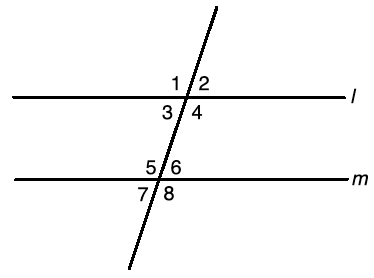
Use this figure to answer the following questions:
a) 
b) 
c) 
d) 
e) 
f) 
g) 
Solution to this Angles Parallel Lines Transversal Geometry practice problem is provided in the video below!
Angle Theorems Parallel Lines and Transversals example problem #2
Use the following figure to find the values of x and y.
Solution to this Angles Parallel Lines Transversal Geometry practice problem is provided in the video below!
Angle Theorems Parallel Lines and Transversals example #3
Use the figure below to solve for the values of x and y.
Solution to this Angles Parallel Lines Transversal Geometry practice problem is provided in the video below!
Angle Theorems Parallel Lines and Transversals example question #4
Use the given figure below to find the values of x and y.
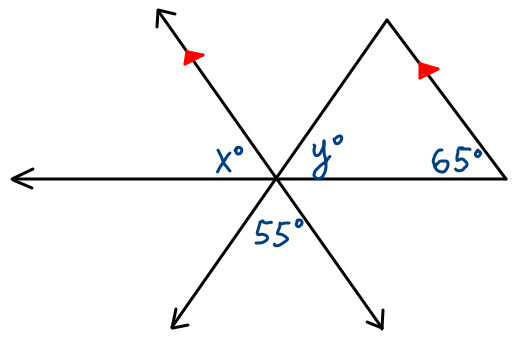
Solution to this Angles Parallel Lines Transversal Geometry practice problem is provided in the video below!
Angle Theorems Parallel Lines and Transversals example problem #5
The figure below shows a polygon with some interior angle measures provided.
Find the values of x and y.
Solution to this Angles Parallel Lines Transversal Geometry practice problem is provided in the video below!
Two-Way Table Data Probability problems
Two Way Table Data Conditional Probability example problem
When insurance companies establish policies for overing screening tests for diseases, one important factor is the value of the test predicting the disease. For example, for a certain type of disease, insurance companies may only cover the test costs if the test improves the prediction of having the disease by 80%. To help decide coverage policy for a new test, use the following data to help decide whether the test should be covered.
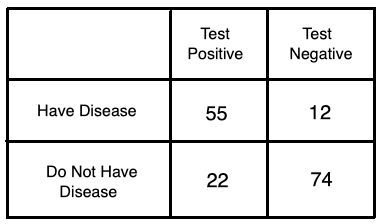
a) Find P(A) = P(Having the disease among everyone)
b) Find P(B) = P(Testing positive for everyone)
c) Find P(A and B) = P(Having the disease and testing positive)
d) Find P(A | B) = P(Having the disease given tested positive)
e) Should the test be covered? What is your conclusion? Justify your answer using the conditional probabilities above.
Solution to this Calculus Two Way Table Data Conditional Probability practice problem is given in the video below!
Vertex Form Quadratic Equation of a Parabola problems
Vertex Form Quadratic Equation of a Parabola example problem
Express the following Parabolic Function Equation in Vertex Form:
f(x) = 12x2 + 24x + 48
Solution to this Vertex Form Quadratic Function practice problem is provided in the video below!
Specific Heat chemistry problems
Specific Heat of Water example question
How much heat, in calories and kilocalories, does it take to raise the temperature of 814 grams of water from 18.0 degrees to 100 ºC?
Solution to this Specific Heat Chemistry practice problem is given in the video below!
Specific Heat of Iridium example problem
A 23.9-gram sample of iridium is heated to 89.7 ºC and then dropped into 20.0 grams of water in a calorimeter. The temperature of the water rises from 20.1 ºC to 22.6 ºC. Calculate the specific heat of iridium.
Solution to this Specific Heat Chemistry practice problem is given in the video below!
Particle Motion calculus problems
Average Velocity of a Particle example question
The velocity, in feet per second, of a particle moving along the x-axis is given by the function v(t) = et + tet. What is the average velocity of the particle from time t = 0 to time t = 3?
Solution to this Particle Motion calculus practice problem is given in the video below!
Number of Times Velocity of a Particle is Zero example problem
The position of an object attached to a spring is given by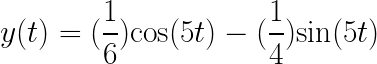 
, where t is time in seconds. In the first 4 seconds, how many times is the velocity of the object equal to 0?
Solution to this Particle Motion calculus practice problem is given in the video below!
Times When a Particle is at Rest example
A particle moves along the x-axis so that at time t ≥ 0 its position is given by 
. At what time t is the particle at rest?
Solution to this Particle Motion calculus practice problem is given in the video below!
Height of a Particle at its Maximum Upward Velocity example question
The height h, in meters, of an object at time t is given by 
. What is the height of the object at the instant when it reaches its maximum upward velocity?
Solution to this Particle Motion calculus practice problem is given in the video below!
Acceleration of a Particle at Time t example problem
A particle moves along the x-axis so that at any time t ≥ 0, its velocity is given by v(t) = 3 + 4.1cos(0.9t). What is the acceleration of the particle at time t = 4?
Solution to this Particle Motion calculus practice problem is given in the video below!
HARD Velocity Acceleration of a Particle example
At time t ≥ 0, the acceleration of a particle moving on the x-axis is a(t) = t + sin(t). At t = 0, the velocity of the particle is -2. For what value of t will the velocity of the particle be zero?
Solution to this Particle Motion calculus practice problem is given in the video below!
Maximum Acceleration of a Particle example question
Find the maximum acceleration attained on the interval 0 ≤ t ≤ 3 by the particle whose velocity is given by
Solution to this Particle Motion calculus practice problem is given in the video below!
Position of a Particle at Time t When its Velocity is First Equal To Zero example problem
A particle moves along the x-axis so that at any time t ≥ 0, its velocity is given by 
. The position of the particle is 3 at time t = 0. What is the position of the particle when its velocity is first equal to 0?
Solution to this Particle Motion calculus practice problem is given in the video below!
Specific Velocity of a Particle using its Acceleration example
A particle moves along the x-axis so that at any time t > 0, its acceleration is given by 
. If the velocity of the particle is 2 at time t = 1, find the velocity of the particle at time t = 2.
Solution to this Particle Motion calculus practice problem is given in the video below!
Time When the Particle is FARTHEST to the Right example question
A particle moves along the x-axis so that its acceleration at any time t is 
. If the initial velocity of the particle is 6, at what time t during the interval 0 ≤ t ≤ 4 is the particle farthest to the right?
Solution to this Particle Motion calculus practice problem is given in the video below!
Rational Equations problems
Solving Rational Equations with Polynomials example question
Solve the following Rational Equation provided below:
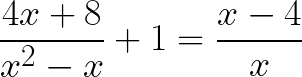
Solution to this Rational Equation with Polynomials practice problem is given in the video below!
Simplifying Polynomial Rational Expressions with Factoring problems
Simplifying Fractions with Polynomials example problem
Simplify the following Fraction Expression to only one term:
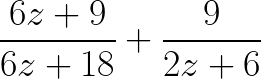
Solution to this Simplification of Fraction with Polynomials practice problem is given in the video below!
Recent Comments