Home » Probability & Statistics
Category Archives: Probability & Statistics
Null Hypothesis Testing statistics problems
Null Hypothesis Test for MEAN example question
A literary critic wants to establish that the mean number of words per sentence, appearing in newly discovered short story is different from 9.1 words. A sample of 36 sentences provided a data with mean of 8.6 words and standard deviation of 1.2 words. Test at a level of significance α = 0.10.
Solution to this Hypothesis Testing Statistics practice problem is given in the video below!
Null Hypothesis Test for PROPORTION example problem
Out of a sample of n = 625 students interviewed, 139 missed at least one class last week. Let p = proportion of students that missed at least one class last week. Conduct a test with the intent of establishing that the proportion of students that missed at least one class last week is greater than 0.20. Test at a level of significance α = 0.05.
Solution to this Hypothesis Testing Statistics practice problem is given in the video below!
Variance problems
Married Couples Expected Value & Variance example question
If 10 married couples are randomly seated at a round table, compute
(a) the Expected number
(b) the Variance
of the number of wives that are seated next to their husbands.
Solution to this Expected Value & Variance practice problem is given in the video below!
Confidence Interval statistics problems
Confidence Interval for MEAN Normal Distribution example question
A manager at a power company monitored the employee time required to process high-efficiency lamp bulb rebates. A random sample of 40 applications gave a sample mean time of 3.8 minutes and a standard deviation of 1.2 minutes. Construct a 90% confidence interval for the mean time to process μ.
Solution to this Confidence Interval Statistics practice problem is given in the video below!
T-Distribution Confidence Interval for MEAN example
From a random sample of size 16, one has calculated the 95% confidence interval for μ (population mean) and obtained the result (39.51, 42.49). What are the x̄ (sample mean) and s (sample standard deviation) for the sample? Assume the population is normal.
Solution to this Confidence Interval Statistics practice problem is given in the video below!
Confidence Interval for PROPORTION Normal Distribution example problem
A telephone survey of 1,000 was taken after movie X came out in the national theater.
a) If 832 liked the movie, with what confidence can it be asserted that 83.2% ± 3% of the adult population liked this movie?
b) If the adult population in the nation is 150 million, what is the interval estimating the total number of people in the nation who liked the movie?
Solution to this Confidence Interval Statistics practice problem is given in the video below!
Two-Way Table Data Probability problems
Two Way Table Data Conditional Probability example problem
When insurance companies establish policies for overing screening tests for diseases, one important factor is the value of the test predicting the disease. For example, for a certain type of disease, insurance companies may only cover the test costs if the test improves the prediction of having the disease by 80%. To help decide coverage policy for a new test, use the following data to help decide whether the test should be covered.
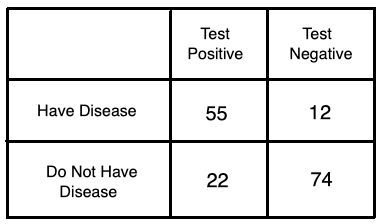
a) Find P(A) = P(Having the disease among everyone)
b) Find P(B) = P(Testing positive for everyone)
c) Find P(A and B) = P(Having the disease and testing positive)
d) Find P(A | B) = P(Having the disease given tested positive)
e) Should the test be covered? What is your conclusion? Justify your answer using the conditional probabilities above.
Solution to this Calculus Two Way Table Data Conditional Probability practice problem is given in the video below!
Tree Diagram Probability problems
Tree Diagram Spinner example problem
A fair spinner showing numbers 1 through 3 of equal area is spun twice. Find the probabilities of the following events:
a) The sum of numbers landed on is odd
b) The sum of numbers landed on is even
c) The two numbers are different
d) Given even first number, the second number is even
e) Given odd first number, the second number is odd
f) The product of the two numbers landed on is less than 6
Solution to this Calculus Tree Diagram Probability practice problem is given in the video below!
Tree Diagram Conditional Probability example question #2
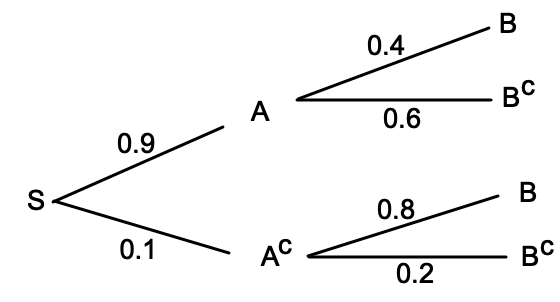
For the given Tree Diagram, calculate the P(A | Bc).
Solution to this Calculus Tree Diagram Probability practice problem is given in the video below!
Tree Diagram Marbles in a Jar probability example
Suppose we have 3 jars: A, B and C. Jar A contains 2 red marbles and 1 blue marble. Jar B contains 1 red marble and 2 blue marbles. Jar C contains 2 red marbles and 2 blue marbles. We select a jar at random. The probability we select A is 
. The probability we select B is . The probability we select C is 
. From the selected jar, we choose 1 marble; all marbles in the jar have the same chance of being selected.
a) What is the probability the chosen marble is red?
b) Given that the chosen marble is red, what is the probability that the selected jar was A?
Solution to this Calculus Tree Diagram Probability practice problem is given in the video below!
Tree Diagram HARD Steroid Drug probability example problem
In recent years, the “Tour de France” cycling race has been plagued with accusations that cyclists have taken steroids to boost their performance. Testing for these steroids has been difficult. The level of steroids that naturally occur in the human body can vary between individuals and the levels can change throughout the day. Testing for the presence of steroids is expensive and time-consuming. Racers are randomly chosen for drug tests. Suppose that 2% of racers have taken an illegal steroid. Assume that if they took the drug, there is a 99% chance that the test will return a “positive” reading and the athlete will be disqualified.
a) Draw a Tree Diagram showing the probabilities for the sequence of events in which an athlete either takes or does not take a drug, and then is tested for the presence of the drug.
b) What is the probability that a randomly chosen cyclist will be steroid-free and will still test positive for steroids?
c) What is the probability that a randomly chosen cyclist will be disqualified due to a “positive” reading?
Solution to this Calculus Tree Diagram Probability practice problem is given in the video below!
Conditional Expectation problems
Geometric Distribution Conditional Expectation Probability example question
A fair die is successively rolled. Let X and Y denote, respectively, the number of rolls necessary to obtain a 6 and a 5.
Find
E [X] ,
E [X Y = 1]
and
E [X Y = 5] .
Solution to this Conditional Expectation Probability practice problem is given in the video below!
Joint Moment Generating Function problems
Joint Moment Generating Function example question
The joint density function of X and Y is given by
f(x, y) = 
Find the Joint Moment Generating Function of X and Y.
Solution to this Joint Moment Generating Function practice problem is given in the video below!
Expected Value problems
Expected Value example question
A box contains 8 green and 4 blue marbles. Two marbles are selected at once without replacement. What is the expected number of green marbles among the selected ones?
a) 1
b) 
c) 
d)
e) 
f) none of the above
Solution to this Expected Value practice problem is given in the video below!
Expected Value example problem #2
You have 5 pairs of shoes. Four of them are worth $30 each, while the fifth is worth $2,000. You select a pair at random. What is the expected value of the pair you have selected?
a) $424
b) $30
c) $50.20
d) $432
e) $1,030
f) none of the above
Solution to this Expected Value practice problem is given in the video below!
Binomial Distribution Expectation example
A sample of 3 items is selected at random from a box containing 20 items of which 4 are defective. Find the expected number of defective items in the sample.
Solution to this Binomial Random Variable Expected Value practice problem is given in the video below!
Hypergeometric Distribution Expectation example question
A ball is chosen at random from each of 5 urns. Each urn contains balls as follows:
urn 1: 1 white, 5 black
urn 2: 3 white, 3 black
urn 3: 6 white, 4 black
urn 4: 2 white, 6 black
urn 5: 3 white, 7 black
Compute the expected number of white balls selected.
Solution to this Hypergeometric Random Variable Expected Value practice problem is given in the video below!
Continuous Distribution Expected Value example problem
The density function of X is given by
f(x) = { 
0 otherwise
If E[X] = 
, find the values of constants 
and 
.
Solution to this Continuous Random Variable Expected Value practice problem is given in the video below!
Independent & Identically Distributed UNIFORM Random Variables Expected Value example
If X1, X2, …, Xn are independent and identically distributed random variables having uniform distributions over (0,1),
find
E [max(X1, …, Xn)]
and
E [min(X1, …,Xn)]
Solution to this Uniform Random Variable Expected Value practice problem is given in the video below!
Joint Distribution Probability Density Function problems
Joint Probability Density Function example question
The joint probability density function of X and Y is given by
f(x,y) = 
a. Find the density function of X
b. Find P(X > Y)
c. Find P(Y > X <
)
Solution to this Joint Probability Density Functions practice problem is given in the video below!
Exponential Distribution Continuous Random Variable problems
Exponential Distribution Probability example question
The time (in hours) required to repair a machine is an exponentially distributed random variable with parameter 
= . What is the probability that a repair time exceeds 2 hours? What is the conditional probability that a repair takes at least 10 hours, given that its duration exceeds 9 hours?
Solution to this Exponential Continuous Random Variable Distribution Probability practice problem is given in the video below!
Normal Distribution Continuous Random Variable problems
Normal Distribution Probability example question
The annual rainfall (in inches) in a certain region is normally distributed with 
= 40, 
= 4. What is the probability that starting with this year, it will take over 10 years before a year occurs having a rainfall of over 50 inches?
Solution to this Normal Continuous Random Variable Distribution Probability practice problem is given in the video below!
Normal Distribution PERCENTILE Probability example problem
The measure of intelligence of a group of people is assumed to be approximately normally distributed with mean 102 and standard deviation 14. If we are told that Tom’s IQ denoted by xT is at the 98th percentile of the IQ distribution of the group of people, find xT.
Solution to this Normal Continuous Random Variable Distribution Probability practice problem is given in the video below!
Uniform Distribution Continuous Random Variable problems
Uniform Distribution Probability example question
You arrive at a bus stop at 10 o’clock, knowing that the bus will arrive at some time uniformly distributed between 10 and 10:30. What is the probability that you will have to wait longer than 10 minutes? If at 10:15 the bus has not yet arrived, what is the probability that you will have to wait at least an additional 10 minutes?
Solution to this Uniform Continuous Random Variable Distribution Probability practice problem is given in the video below!
Independent & Identically Distributed UNIFORM Random Variables Expected Value example
If X1, X2, …, Xn are independent and identically distributed random variables having uniform distributions over (0,1),
find
E [max(X1, …, Xn)]
and
E [min(X1, …,Xn)]
Solution to this Uniform Random Variable Expected Value practice problem is given in the video below!
Continuous Distribution Random Variable problems
Continuous Distribution Probability example question
X is a continuous random variable with probability density function given by
f(x) = { 
0 otherwise
a. Find the value of C
b. What is the probability that X > 1?
Solution to this Continuous Random Variable Distribution Probability practice problem is given in the video below!
Hypergeometric Distribution Discrete Random Variable problems
Hypergeometric Distribution Probability example question
Out of 100 students qualifying for an exam, 20 were drawn randomly. If 65 out of 100 qualified students are male, what is the probability that 14 out of 20 chosen students are female?
Solution to this Hypergeometric Discrete Random Variable Distribution Probability practice problem is given in the video below!
Negative Binomial Distribution Discrete Random Variable problems
Negative Binomial Distribution Probability example question
An interviewer is given a list of potential people she can interview. If the interviewer needs to interview 5 people and if each person (independently) agrees to be interviewed with probability , what is the probability that her list of potential people will enable her to obtain her necessary number of interviews if the list consists of 5 people or 8 people?
Solution to this Negative Binomial Discrete Random Variable Distribution Probability practice problem is given in the video below!
Poisson Distribution Discrete Random Variable problems
Poisson Distribution Probability example question
Suppose that the number of accidents occurring on a highway each day is a Poisson random variable with parameter = 3.
(a) Find the probability that 3 or more accidents occur today
(b) Repeat part (a) under the assumption that at least 1 accident occurs today
Solution to this Poisson Discrete Random Variable Distribution Probability practice problem is given in the video below!
Geometric Distribution Discrete Random Variable problems
Geometric Distribution Probability example question
Consider a roulette wheel consisting of 38 numbers – 1 through 36, 0, and double 0. If Smith always bets that the outcome will be one of the numbers 1 through 12, what is the probability that Smith will lose his first 5 bets? What is the probability that his first win will occur on his fourth bet?
Solution to this Geometric Discrete Random Variable Distribution Probability practice problem is given in the video below!
Binomial Distribution Discrete Random Variable problems
Binomial Distribution Probability example question
A multiple choice exam consists of 4 questions. Each question has 5 possible answers, exactly one of which is correct. Donald decides to guess all questions on the exam. What is the probability that he will answer exactly two questions correctly?
a) 0.1024
b) 0.9744
c) 0.2048
d) 0.1536
e) 0.0256
f) none of the above
Solution to this Binomial Discrete Random Variable Distribution Probability practice problem is given in the video below!
Hard Binomial Distribution Probability example problem
The efficacy of the mumps vaccine is about 80%; that is, 80% of those receiving the mumps vaccine will not contract the disease when exposed. Assume that each person’s response to the mumps is independent of another person’s response.
a) Find the probability that at least one exposed person will get the mumps if 10 people are exposed.
b) How many vaccinated people must be exposed to the mumps before the probability that at least one person will contract the disease is at least 0.95?
Solution to this Binomial Discrete Random Variable Distribution Probability practice problem is given in the video below!
Independent Events Probability problems
Independent Events Probability example question
Two independent events have P(A) = P(B) = 0.3. What is the P(A 
B)?
a) 0.09
b) 0.91
c) 0.49
d) 0.51
e) 0.6
f) none of the above
Solution to this Independent Events Probability practice problem is given in the video below!
Independent Events Probability example problem
For two independent events we know that P(A) = 0.7 and P(A 
B) = 0.21. What is P(B)?
a) 0.7
b) 0.6
c) 0.5
d) 0.4
e) 0.3
f) none of the above
Solution to this Independent Events Probability practice problem is given in the video below!
Independent Events Probability example
A car of brand X has a transmission which fails with probability 0.6 and brakes which fail with probability 0.3; the two kinds of failures occur independently. At any given day, what is the probability that exactly one of the failures occurs while driving the car of brand X?
a) 0.72
b) 0.28
c) 0.46
d) 0.54
e) 0.90
f) none of the above
Solution to this Independent Events Probability practice problem is given in the video below!
Probability of Outcomes problems
Coin Flip Outcome Probability example question
In an experiment, a coin is tossed until either the same side comes up twice in a row, or the coin has been tossed four times. How many outcomes are there?
a) 6
b) 8
c) 10
d) 16
e) this experiment never stops
f) none of the above
Solution to this Outcomes Probability practice problem is given in the video below!
Coin Flip: Unfair Toss Probability example problem
An unfair coin with P(H) = 0.9 is tossed independently 5 times. What is the probability that the first, third, and fifth tosses are Heads, and all the others are Tails?
a) 0.0243
b) 0.00243
c) 0.243
d) 0.0729
e) 0.00729
f) none of the above
Solution to this Outcomes Probability practice problem is given in the video below!
Unfair Die Toss Probability example
An unfair die is such that the outcomes 1, 2, 3, 5 are equally likely, 4 is half as likely as 2, and 6 is four times as likely as 5. What is the probability of having a 4?
a) 
b) 
c) 
d) 
e) 
f) none of the above
Solution to this Outcomes Probability practice problem is given in the video below!
Coin & Die Toss Outcome Probability example question
In an experiment, a coin is tossed, and if the outcome is Heads, then a die is rolled. If the outcome is Tails, the experiment stops. How many outcomes are possible in this experiment?
a) 6
b) 7
c) 12
d) 14
e) 15
f) none of the above
Solution to this Outcomes Probability practice problem is given in the video below!
Choices of Pencil Colors Probability example problem
You have 4 white pencils and 6 grey pencils. You select two pencils at random. What is the probability that the two pencils are of the same color?
a) 
b)
c)
d) 
e) 
f) none of the above
Solution to this Outcomes Probability practice problem is given in the video below!
Rule of Product Probability problems
Rule of Product Probability example question
A quiz contains one Algebra problem, one Geometry problem, and one Probability problem. There are 4 Algebra problems, 5 Geometry problems, and 2 Probability problems available to make the quiz. How many different quizzes are possible?
a) 20
b) 40
c) 
d) 
e) 10
f) none of the above
Solution to this Rule of Product Probability practice problem is given in the video below!
Permutations & Combinations problems
Permutation Probability example question
You are trying to form a unique string of three letters from the list {A, B, C, D, E} so that the first two letters are distinct. How many strings are there?
a) 10
b) 16
c) 14
d) 100
e) 125
f) none of the above
Solution to this Permutation Probability practice problem is given in the video below!
Combination Probability example problem
Four tennis players decide to play one “doubles” game each day (two players per team) until all possible combinations are used. How many days will they play?
a) 1
b) 3
c) 6
d) 12
e) 24
f) none of the above
Solution to this Combination Probability practice problem is given in the video below!
Combination Probability example
A Geometry class consists of 23 juniors and 44 sophomores. A committee of 5 students is chosen at random. What is the probability that no juniors are chosen?
a) 
b)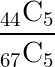 
c)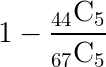 
d)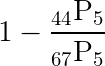 
e) 0
f) none of the above
Solution to this Combination Probability practice problem is given in the video below!
Combination Probability example question
A jury of five must decide whether Rick will pass his Probability class. In order for Rick to pass, at least four of the jurors must be in favor. In how many ways can Rick pass his class?
a) 16
b) 6
c) 5
d) 4
e) 32
f) none of the above
Solution to this Combination Probability practice problem is given in the video below!
Combination Probability example problem
You have 25 identical flowers in your garden, and you want to remove any 5 of them. In how many ways can you choose the flowers?
a) 252
b) 525
c) 
d) 
e) 
f) none of the above
Solution to this Combination Probability practice problem is given in the video below!
Permutation-Combination example
You have 35 different pancakes to choose from. You want to order a stack of three pancakes. If you care about the ordering of the pancakes you get, how many choices are possible? (For example, raspberry/blueberry/pecan is different from raspberry/pecan/blueberry).
a) 
b) 75
c) 353
d) 335
e) 
f) none of the above
Solution to this Permutation-Combination Probability practice problem is given in the video below!
Permutation-Combination example problem #2
Calculate the maximum number of 3rd Great Grandparents each person has by using Factorials, Permutations and Combinations.
Solution to this Permutation-Combination Probability practice example is given in the video below!
Percent Probability problems
Probability with Percentages example question
A college survey shows that 10% of freshmen, 15% of sophomores, 60% of juniors, and 85% of seniors like Probability. Given that 30% of all students are freshmen, 30% are sophomores, 20% are juniors, and 20% are seniors, what percentage of all students in the college like Probability?
a) 0.635
b) 0.535
c) 0.465
d) 0.365
e) 0.235
Solution to this Percent Probability practice problem is given in the video below!
Probability & Statistics problems (complete Playlist)
Find many different Probability and Statistics examples and practice problems that may be useful in your Algebra, Geometry, Precalculus, or Calculus courses.
SOA Exam P CAS Exam 1 Expected Value Variance Standard Deviation probability problems
Multiple Moment Generating Functions MGF example question
A company insures homes in three cities, J, K and L. Since sufficient distance separates the cities, it is reasonable to assume that the losses occurring in these cities are independent. The moment generating functions for the loss distributions of the cities are
Let X represent the combined losses from the three cities. Calculate 
.
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
Expected Value & Probability Density Function PDF example problem
Let X be a continuous random variable with density function
{ 
Calculate the expected value of X.
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
Moment Generating Function MGF example
Let X1 , X2 , X3 be a random sample from a discrete distribution with probability function
{ 
Determine the moment generating function, M(t), of 
.
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
Expected Value & Probability Density Function PDF word problem
An insurance company’s monthly claims are modeled by a continuous, positive random variable X, whose probability density function is proportional to
Determine the company’s expected monthly claims.
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
Percentiles & Probability Density Function PDF example question
An insurer’s annual weather related loss, X, is a random variable with density function
{ 
Calculate the difference between the 30th and 70th percentiles of X.
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
Standard Deviation & Moment Generating Function MGF example problem
An actuary determines that the claim size for a certain class of accidents is a random variable, X, with a moment generating function
Determine the standard deviation of the claim size for this class of accidents.
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
Standard Deviation Table example
A probability distribution of the claim sizes for an auto insurance policy is given in the table below:
| Claim Size | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| Probability | .15 | .10 | .06 | .20 | .10 | .10 | .30 |
What percentage of the claims are within one standard deviation of the mean claim size?
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
Variance & Cumulative Distribution Function CDF example question
A random variable has the cumulative distribution function
{ 
Calculate the variance of X.
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
Variance word problem
A recent study indicates that the annual cost of maintaining and repairing a car in a town to Ontario averages 200 with a variance of 260. If a tax of 20% is introduced on all items associated with the maintenance and repair of cars (i.e., everything is made 20% more expensive), what will be the variance of the annual cost of maintaining and repairing a car?
Solution to this Society of Actuaries Exam P practice problem is given in the video below!
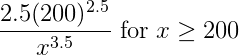
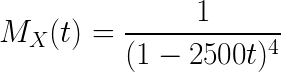
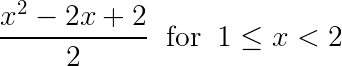
Recent Comments