Home » Trigonometric Equations
Category Archives: Trigonometric Equations
Trigonometric Functions WORD problems
Ferris Wheel trigonometry word problem
The Ferris wheel at Navy Pier has a diameter of 140 feet. It stands 10 feet off the ground. The wheel has 40 gondolas that seat six passengers each. It takes about 6 minutes for the Navi Pier Ferris wheel to complete one rotation.
Draw a diagram of the Navy Pier Ferris wheel and the boarding platform. Fill in the necessary information. Sketch the graph. Write a cosine equation for your curve. Write a sine equation for your curve.
Answer the following questions:
i. What is the circumference of the wheel?
ii. At what speed is the wheel traveling? Please answer in feet / second.
iii. If you begin your ride at the base of the wheel, what is the height after 1 minute? 4 minutes?
iv. At what approximate time(s) will you reach the following heights?
a) 100 ft
b) 240 ft
v. What is the length of the arc traveled by the Navy Pier Ferris wheel from the 4 o’clock to the 7 o’clock position?
Solution to this Trigonometric Function word practice problem is provided in the video below!
Roller Coaster trigonometry problem
A portion of a roller coaster is to be built in the shape of a sinusoid. You have been hired to calculate the lengths of the horizontal and vertical timber supports to be used.
a. The high and low points on the track are separated by 50 meters horizontally and 30 meters vertically. The low point is 3 meters below the ground. Letting y be the number of meters the track is above the ground and x the number of meters horizontally from the high point, write an equation expressing y in terms of x.
b. How long is the vertical timber at the high point? At x = 4 m? At x = 32 m?
c. Where does the track first go below ground?
Solution to this Trigonometric Function example practice problem is provided in the video below!
Steamboat trigonometry example word problem
Mark Twain sat on the deck of a river steamboat. As the paddlewheel turned, a point on the paddle blade moved in such a way that its distance, d, from the water’s surface was a sinusoidal function of time. When his stopwatch read 4 seconds, the point was at its highest, 16 feet above the water’s surface. The wheel’s diameter was 18 feet, and it completed a revolution every 10 seconds.
a. Sketch a graph of the sinusoid
b. Write the equation of the sinusoid
c. How far above the surface was the point when Mark’s stopwatch read:
i. 5 seconds
ii. 17 seconds
d. What is the first positive value of time at which the point was at the water’s surface? At that time, was it going into or coming out of the water? Explain.
Solution to this Trigonometric Function example word problem is provided in the video below!
Temperature trigonometry word problem
The max temperature in Buenos Aires is on January 15 and is 33 degrees Celsius. The minimum temperature is on July 16 (day 197) and is 9 degrees Celsius. (Assume the period is 365 days).
a) Sketch the temperature as a function of time
b) Find the equation for the temperature, T, as a function of time, t.
c) What is the temperature on Mother’s Day, May 10?
d) Give the dates during a one year period when the temperature is below 18 degrees Celsius.
Solution to this Trigonometric Function example word problem is provided in the video below!
Trigonometric Equations with Angle Sum, Difference, Multiple, Half-Angle Formulas problems
Trigonometric Equation Double-Angle and Product-To-Sum example
Solve the following Trigonometric Equations using Double-Angle and Product-To-Sum formulas:
sin2θ – sinθ = 0
cosx + cos3x = cos2x
Solution to this Trigonometric Equation Double-Angle Product-To-Sum practice problem is provided in the video below!
Trigonometric Equations problems
Solution to Trigonometric Equation example question
Solve the following Trigonometric Equations:
![]()
tan(3t) = 1
2cos2u = cosu
![]()
ln(sinx) = 0
Solution to this Trigonometric Equations practice problem is provided in the video below!
Trigonometric Identity Proof problems
Trigonometric Identity Proofs example problem #1
Show that
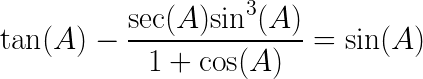
Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proof example question #2
Show that the following equation is valid.
![]()
Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proofs example #3
Prove the validity of the following equation.
![]()
Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proof example problem #4
Prove that
![]()
Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proofs example question #5
Prove the following identity.

Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proof example #6
Show that the following identity holds.
![]()
Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proofs example problem #7
Prove the following identity.

Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proof example question #8
Verify the given identity.

Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proofs example #9
Show that the identity given below is valid.

Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proof example problem #10
Verify the given three Trigonometric Identities:
(a)

(b)
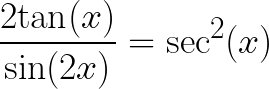
(c)

Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proof example question #11
Show that the following Trigonometric Identity is true:

Solution to this Trigonometric Identity Proof practice problem is given in the video below!
Trigonometric Identity Proof example question #12
Verify that the following Trigonometric Identities hold:
a. sin(-x) = -sin(x)
b. ![]()
c. 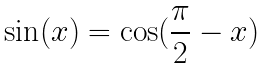
d. sin(2x) = 2sin(x)cos(x)
e. ![]()
f. cos(-x) = cos(x)
g. ![]()
Solution to this Trigonometric Identity Proof practice example question is given in the video below!
Recent Comments