Sphere Related Rates example problem
The radius of a sphere is r when the time is t seconds. Find the radius when the rate of change of the surface area and the rate of change of the radius are equal.
Solution to this Calculus Related Rates practice problem is given in the video below!
Balloon Related Rates example question
Gas is escaping from a spherical balloon at the rate of 4 cubic feet per minute. How fast is the surface area of the balloon shrinking when the radius of the balloon is 4 feet?
Solution to this Calculus Related Rates practice problem is given in the video below!
Approaching Cars Related Rates example
A car is traveling at 50 miles per hour due south at a point ![]() mile north of an intersection. A police car is traveling at 40 miles per hour due west at a point
mile north of an intersection. A police car is traveling at 40 miles per hour due west at a point ![]() mile east of the same intersection. At that instant, the radar in the police car measures the rate at which the distance between the two cars is changing. What does the radar gun register?
mile east of the same intersection. At that instant, the radar in the police car measures the rate at which the distance between the two cars is changing. What does the radar gun register?
Solution to this Calculus Related Rates practice problem is given in the video below!
Sliding Ladder Related Rates example problem
A 10-foot ladder leans against the side of the building. If the top of the ladder begins to slide down the wall at the rate of 2 feet per second, how fast is the bottom of the ladder sliding away from the wall when the top of the ladder is 8 feet off the ground?
Solution to this Calculus Related Rates practice problem is given in the video below!
Oil Spill Related Rates example question
An oil tanker has an accident and oil pours out at the rate of 150 gallons per minute. Suppose that the oil spreads onto the water in a circle at a thickness of ![]() inches. Given that 1 cubic inch equals 7.5 gallons, determine the rate at which the radius of the spill is increasing when the radius reaches 500 feet.
inches. Given that 1 cubic inch equals 7.5 gallons, determine the rate at which the radius of the spill is increasing when the radius reaches 500 feet.
Solution to this Calculus Related Rates practice problem is given in the video below!
Trigonometry Related Rates example
A spectator at an air show is trying to follow the flight of a jet. The jet follows a straight path in front of the observer at 540 miles per hour. At its closest approach, the jet passes 600 feet in front of the person. Find the maximum rate of change of the angle between the spectator’s line of sight and a line perpendicular to the flight path, as the jet flies by.
Solution to this Calculus Related Rates practice problem is given in the video below!
Complex Trigonometry Related Rates example problem
Two buildings, of height 20 feet and 40 feet, are 60 feet apart. Suppose that the intensity of light at a point between the buildings is proportional to the angle ![]() in the figure. If a person is moving from right to left at 4 feet per second, at what rate is this angle
in the figure. If a person is moving from right to left at 4 feet per second, at what rate is this angle ![]() changing when the person is exactly halfway between the two buildings?
changing when the person is exactly halfway between the two buildings?
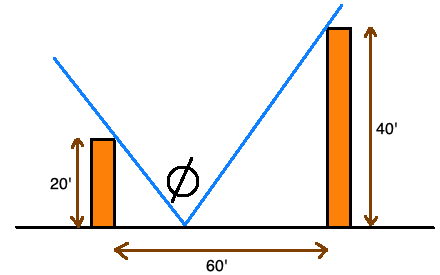
Solution to this Calculus Related Rates practice problem is given in the video below!
Cone Related Rates example question
Water is running out of a conical funnel at the rate of 1 cubic inch per second. If the radius of the base of the funnel is 4 inches and the height is 8 inches, find the rate at which the water level is dropping when it is 2 inches from the top.
Solution to this Calculus Related Rates practice problem is given in the video below!
Pulley example Related Rates example
A weight W is attached to a rope 50-foot-long that passes over a pulley at a point P, 20 feet above the ground. The other end of the rope is attached to a truck at a point A, 2 feet above the ground. If the truck moves away at the rate of 9 feet per second, how fast is the weight rising when it is 6 feet above the ground?
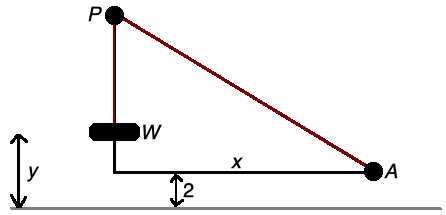
Solution to this Calculus Related Rates practice problem is given in the video below!
Shadow Related Rates example problem
Suppose a 6-ft-tall person is x feet away from an 18-ft-tall lamppost. If the person is moving away from the lamppost at a rate of 2 feet per second, at what rate is the length of the shadow changing?
Solution to this Calculus Related Rates practice problem is given in the video below!
Kite Related Rates example question
A boy is flying a kite at a height of 150 feet. If the kite moves horizontally away from the boy at 20 feet per second, how fast is the string being paid out when the kite is 250 feet from him?
Solution to this Calculus Related Rates practice problem is given in the video below!
Curve Related Rates example
If a point moves along the curve ![]() ,
,
at what point is the y-coordinate changing twice as fast as the x-coordinate?
Solution to this Calculus Related Rates practice problem is given in the video below!
Boat Related Rates example problem
A barge, whose deck is 10 feet below the level of the dock, is being drawn in by means of a cable attached to the deck and passing through a ring on the dock. When the barge is 24 feet away and approaching the dock at ![]() feet per second, how fast is the cable being pulled in? (Neglect any sag in the cable.)
feet per second, how fast is the cable being pulled in? (Neglect any sag in the cable.)
Solution to this Calculus Related Rates practice problem is given in the video below!
HARD Related Rates Clock example question
The minute and hour hands of a clock are 15 cm and 10 cm long, respectively. Find the rates at which the angle and distance between the tips of these hands of a clock are changing when the time on the clock shows 12:30 p.m.
Solution to this Calculus Related Rates practice problem is given in the video below!
Recent Comments